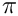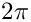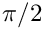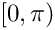YODA Namespace Reference

Anonymous namespace to limit visibility. More...

Namespaces
namespace	YODAConcepts

Classes
class	AnalysisObject
	AnalysisObject is the base class for histograms and scatters. More...
class	AnnotationError
	Errors relating to insufficient (effective) statistics. More...
class	AOReader
class	AOReader< BinnedDbn< DbnN, AxisT... > >
class	AOReader< BinnedEstimate< AxisT... > >
class	AOReader< Counter >
class	AOReader< Estimate0D >
class	AOReader< ScatterND< N > >
class	AOReaderBase
struct	ArithmeticWrapper
	Arithmetic wrapper to emulate inheritance from arithmetic types. More...
class	Axis
	Discrete axis with edges of non-floating-point-type. More...
class	Axis< T, isCAxis< T > >
	Continuous axis with floating-point-type edges. More...
class	Bin
	generic Bin version that derives from BinBase More...
class	Bin< 1, T, BinningT >
	CRTP specialisation in 1D. More...
class	Bin< 2, T, BinningT >
	CRTP specialisation in 2D. More...
class	Bin< 3, T, BinningT >
	CRTP specialisation in 3D. More...
class	BinBase
	Bin base class consisting of mix of histogram bin content and space characteristics of this bin (widths, min, max, mid, etc...) More...
struct	BinEstimator
	Bin estimator. More...
class	BinnedDbn
	User-facing BinnedDbn class in arbitrary dimension. More...
class	BinnedDbn< 1, AxisT >
	Specialisation of the BinnedDbn for a 1D histogram. More...
class	BinnedDbn< 2, AxisT >
	Specialisation of the BinnedDbn for a 1D profile. More...
class	BinnedDbn< 2, AxisT1, AxisT2 >
	Specialisation of the BinnedDbn for a 2D histogram. More...
class	BinnedDbn< 3, AxisT1, AxisT2 >
	Specialisation of the BinnedDbn for a 2D profile. More...
class	BinnedDbn< 3, AxisT1, AxisT2, AxisT3 >
	Specialisation of the BinnedDbn for a 3D histogram. More...
class	BinnedDbn< 4, AxisT1, AxisT2, AxisT3 >
	Specialisation of the BinnedDbn for a 2D profile. More...
class	BinnedEstimate
	Forward declaration. More...
class	BinnedEstimate< AxisT >
	Specialisation of the BinnedEstimate for a 1D histogram. More...
class	BinnedEstimate< AxisT1, AxisT2 >
	Specialisation of the BinnedEstimate for a 2D BinnedEstimate. More...
class	BinnedEstimate< AxisT1, AxisT2, AxisT3 >
	Specialisation of the BinnedEstimate for a 3D BinnedEstimate. More...
class	BinnedStorage
	BinnedStorage, stores the bins and coordinates access to them. More...
class	Binning
class	BinningError
	Error for general binning problems. More...
class	BinsVecWrapper
	Vector wrapper used to interact with bins vectors. Able to hide overflow and hidden bins. More...
struct	CIterable
struct	CIterable< T, std::void_t< decltype(std::declval< typename T::const_iterator >())> >
struct	CmpFloats
	Functor to compare two floating point numbers and return whether they are fuzzily equivalent. More...
class	Counter
	A weighted counter. More...
class	Dbn
	User-facing Dbn class inheriting from DbnBase. More...
class	Dbn< 0 >
	Partial template specialisation for Dbn0D. More...
class	Dbn< 1 >
	Partial template specialisation with CRTP for x-methods. More...
class	Dbn< 2 >
	Partial template specialisation with CRTP for x- and y-methods. More...
class	Dbn< 3 >
	Partial template specialisation with CRTP for x-, y- and z-methods. More...
class	DbnBase
	A 1D distribution. More...
class	DbnStorage
	All histograms can be instantiated through this alias. More...
struct	defaultAdapter
	Type to adapter mapping used when user didn't provide type adapter. More...
struct	defaultAdapter< DbnN, BinT< N, Dbn< DbnN >, BinningT > >
	Default fill adapter for binned type Dbn<N> More...
struct	defaultAdapter< FillDim, BinT< N, double, BinningT > >
	Default fill adapter for binned type double. More...
struct	Derefable
	SFINAE definition of dereferenceability trait, cf. Boost has_dereference. More...
struct	Derefable< T, std::void_t< decltype(*std::declval< T >())> >
struct	DerefableToAO
	SFINAE struct to check for dereferencing to an AnalysisObject (reference) at compile time. More...
struct	DerefableToAO< T, typename std::conditional< std::is_base_of< AnalysisObject, typename std::decay< decltype(*std::declval< T >()) >::type >::value, AnalysisObject, void >::type >
class	EdgeHandler
	Specialised wrapper for a vector of type T. More...
class	EdgeHandlerBase
	Base wrapper around a vector of edges. More...
class	Estimate
	A point estimate (base class for the Estimate) More...
class	Estimate0D
	An estimate in 0D. More...
class	EstimateStorage
	EstimateStorage convenience class based on BinnedStorage. More...
class	Exception
	Generic unspecialised YODA runtime error. More...
class	Fillable
	A base class for all fillable objects. More...
class	FillableStorage
	FillableStorage, introduces FillAdapterT on top of BinnedStorage base class. More...
class	H5DataSetReader
	Helper class to extract information from YODA_H5::DataSets. More...
class	H5DataSetWriter
	A helper class to deal with chunking of H5 datasets. More...
class	H5FileManager
	Helper class to extract AO information from a H5 file. More...
struct	hasFillDim
struct	hasFillDim< T, std::void_t< decltype(typename T::FillDim{})> >
struct	Iterable
struct	Iterable< T, std::void_t< std::decay_t< decltype(std::begin(std::declval< const T & >()))>, std::decay_t< decltype(std::end(std::declval< const T & >()))> > >
struct	LinBinEstimator
	Linear bin estimator. More...
class	LogBinEstimator
	Logarithmic bin estimator. More...
class	LogicError
	Error for places where it should not have been possible to get to! More...
class	Point
	Base class for all Point*Ds, providing generic access to their numerical properties. More...
class	PointBase
	The base for an N-dimensional data point to be contained in a Scatter<N> More...
class	PointND
class	PointND< 1 >
	A 1D data point to be contained in a Scatter1D. More...
class	PointND< 2 >
	A 2D data point to be contained in a Scatter2D. More...
class	PointND< 3 >
	A 3D data point to be contained in a Scatter3D. More...
struct	Pushable
struct	Pushable< T, VAL, std::void_t< decltype(std::declval< T >().push_back(std::declval< VAL >()))> >
class	RangeError
	Error for e.g. use of invalid bin ranges. More...
class	Reader
	Pure virtual base class for various output writers. More...
class	ReaderFLAT
	Persistency reader from YODA flat text data format. More...
class	ReaderH5
	Persistency reader from YODA text data format. More...
class	ReadError
	Error for file reading errors. More...
class	ReaderYODA
	Persistency reader from YODA text data format. More...
class	Scatter
	A base class for common operations on scatter types (Scatter1D, etc.) More...
class	ScatterND
	A generic data type which is just a collection of n-dim data points with errors. More...
class	Transformation
struct	TypeID
	Returns the type ID as a character sequence. More...
struct	TypeID< std::string >
	Specialisation for type string. More...
class	UserError
	Error for problems introduced outside YODA, to put it nicely. More...
class	WeightError
	Errors relating to event/bin weights. More...
class	Weights
	A named, vectorised generalisation of an event weight. More...
class	WriteError
	Error for file writing errors. More...
class	Writer
	Pure virtual base class for various output writers. More...
class	WriterFLAT
	Persistency writer for flat text format. More...
class	WriterH5
	Persistency writer for YODA H5 format. More...
class	WriterYODA
	Persistency writer for YODA flat text format. More...
class	WriterYODA1
	Legacy persistency writer for YODA1-style flat text format. More...
struct	XAxisMixin
	CRTP mixin introducing convenience aliases along X axis. More...
struct	XBinMixin
	CRTP mixin introducing convenience aliases along X axis. More...
struct	XDbnMixin
	CRTP mixin introducing convenience aliases along X axis. More...
struct	XDirectionMixin
	CRTP mixin introducing convenience aliases along X axis. More...
struct	XStatsMixin
	CRTP mixin introducing convenience aliases to access statistics along X axis. More...
struct	YAxisMixin
	CRTP mixin introducing convenience aliases along Y axis. More...
struct	YBinMixin
	CRTP mixin introducing convenience aliases along Y axis. More...
struct	YDbnMixin
	CRTP mixin introducing convenience aliases along Y axis. More...
struct	YDirectionMixin
	CRTP mixin introducing convenience aliases along Y axis. More...
struct	YStatsMixin
	CRTP mixin introducing convenience aliases to access statistics along Y axis. More...
struct	ZAxisMixin
	CRTP mixin introducing convenience aliases along Z axis. More...
struct	ZBinMixin
	CRTP mixin introducing convenience aliases along Z axis. More...
struct	ZDbnMixin
	CRTP mixin introducing convenience aliases along Z axis. More...
struct	ZDirectionMixin
	CRTP mixin introducing convenience aliases along Z axis. More...
struct	ZStatsMixin
	CRTP mixin introducing convenience aliases to access statistics along Z axis. More...

Typedefs
using	AO = AnalysisObject
	Convenience alias.
using	Dbn0D = Dbn< 0 >
	User-friendly aliases.
using	Dbn1D = Dbn< 1 >
using	Dbn2D = Dbn< 2 >
using	Dbn3D = Dbn< 3 >
template<typename A1 >
using	BinnedHisto1D = BinnedHisto< A1 >
	Define dimension-specific short-hands (Cython sugar)
template<typename A1 , typename A2 >
using	BinnedHisto2D = BinnedHisto< A1, A2 >
template<typename A1 , typename A2 , typename A3 >
using	BinnedHisto3D = BinnedHisto< A1, A2, A3 >
template<size_t N>
using	HistoND = typename HistoMaker< std::make_index_sequence< N > >::type
using	Histo1D = BinnedHisto< double >
	User-friendly familiar names (continuous axes only)
using	Histo2D = BinnedHisto< double, double >
using	Histo3D = BinnedHisto< double, double, double >
using	Point1D = PointND< 1 >
	User-familiar alias.
using	Point2D = PointND< 2 >
using	Point3D = PointND< 3 >
using	Point4D = PointND< 4 >
template<typename A1 >
using	BinnedProfile1D = BinnedProfile< A1 >
	Define dimension-specific short-hands (Cython sugar)
template<typename A1 , typename A2 >
using	BinnedProfile2D = BinnedProfile< A1, A2 >
template<typename A1 , typename A2 , typename A3 >
using	BinnedProfile3D = BinnedProfile< A1, A2, A3 >
template<size_t N>
using	ProfileND = typename ProfileMaker< std::make_index_sequence< N > >::type
	User-friendly name for the N-dimensional profile with all-continuous axes.
using	Profile1D = BinnedProfile< double >
	User-friendly familiar names (continuous axes only)
using	Profile2D = BinnedProfile< double, double >
using	Profile3D = BinnedProfile< double, double, double >
template<typename T >
using	EdgeHandlerPtr = typename std::shared_ptr< EdgeHandler< T > >
	Convenience aliases.
using	EdgeHandlerBasePtr = typename std::shared_ptr< EdgeHandlerBase >
Define dimension-specific short-hands
template<typename... AxisTypes>
using	BinnedHisto = BinnedDbn< sizeof...(AxisTypes), AxisTypes... >
template<typename... AxisTypes>
using	BinnedProfile = BinnedDbn< sizeof...(AxisTypes)+1, AxisTypes... >
Convenience aliases
template<typename A1 >
using	BinnedEstimate1D = BinnedEstimate< A1 >
	Define dimension-specific short-hands (Cython sugar)
template<typename A1 , typename A2 >
using	BinnedEstimate2D = BinnedEstimate< A1, A2 >
template<typename A1 , typename A2 , typename A3 >
using	BinnedEstimate3D = BinnedEstimate< A1, A2, A3 >
template<size_t N>
using	EstimateND = typename EstimateMaker< std::make_index_sequence< N > >::type
using	Estimate1D = BinnedEstimate< double >
using	Estimate2D = BinnedEstimate< double, double >
using	Estimate3D = BinnedEstimate< double, double, double >
User friendly aliases
using	Scatter1D = ScatterND< 1 >
using	Scatter2D = ScatterND< 2 >
using	Scatter3D = ScatterND< 3 >
using	Scatter4D = ScatterND< 4 >
using	S1D = Scatter1D
using	S2D = Scatter2D
using	S3D = Scatter3D
using	S4D = Scatter4D
Convenient aliases
template<size_t N>
using	Trf = Transformation< N >
Helper methods to probe continuous/discrete axis properties.
template<typename... EdgeT>
using	all_CAxes = typename std::conjunction< std::is_floating_point< EdgeT >... >
template<typename... EdgeT>
using	enable_if_all_CAxisT = std::enable_if_t< all_CAxes< EdgeT... >::value >
	Checks if all edge types are continuous.
template<typename EdgeT >
using	enable_if_CAxisT = std::enable_if_t< std::is_floating_point< EdgeT >::value, EdgeT >
	Checks if edge type is continuous and returns edge type.
template<typename EdgeT >
using	enable_if_DAxisT = std::enable_if_t<!std::is_floating_point< EdgeT >::value, EdgeT >
	Checks if edge type is discrete and returns edge type.

Enumerations
enum	Sign { MINUS = -1 , ZERO = 0 , PLUS = 1 }
	Enum for signs of numbers. More...

Functions
template<typename CoordT >
double	nullifyIfDiscCoord (CoordT &&, std::false_type, double null=0.0)
	Nullifies coordinate if it is discrete.
template<typename CoordT >
double	nullifyIfDiscCoord (CoordT &&coord, std::true_type, double=0.0)
template<typename... Args>
bool	containsNan (const std::tuple< Args... > &coords)
	Checks if a coordinate tuple has a nan.
std::string	version ()
	Namespaced version string function.
template<size_t N>
DbnBase< N >	operator+ (DbnBase< N > first, const DbnBase< N > &second)
	Add two DbnBases.
template<size_t N>
DbnBase< N >	operator+ (DbnBase< N > first, DbnBase< N > &&second)
	Add two DbnBases.
template<size_t N>
DbnBase< N >	operator- (DbnBase< N > first, const DbnBase< N > &second)
	Subtract one DbnBase from another one.
template<size_t N>
DbnBase< N >	operator- (DbnBase< N > first, DbnBase< N > &&second)
	Subtract one DbnBase from another one.
Reader &	mkReader (const std::string &format_name)
	Factory function to make a reader object by format name or a filename.
template<typename T >
YODA_H5::DataSet	H5DataSet (YODA_H5::File &h5file, const string &label, vector< T > &&data, bool compress)
	Helper method to construct and fill a YODA_H5::DataSet.
template<typename T >
YODA_H5::DataSet	H5DataSet (YODA_H5::File &h5file, const string &label, size_t nrows, size_t chunksize, bool compress)
	Helper method to construct an empty YODA_H5::DataSet.
std::string	getLibPath ()
	Get the path to the directory containing libYODA.
std::string	getDataPath ()
	Get the path to the installed share/YODA/ data directory.
std::vector< std::string >	getYodaDataPath ()
	YODA data paths.
std::ostream &	operator<< (std::ostream &out, const Weights &w)
	Standard text representaion.
Writer &	mkWriter (const std::string &format_name)
	Factory function to make a writer object by format name or a filename.
Combining BinnedDbn objects: global operators
template<size_t DbnN, typename... AxisT>
BinnedDbn< DbnN, AxisT... >	operator+ (BinnedDbn< DbnN, AxisT... > first, BinnedDbn< DbnN, AxisT... > &&second)
	Add two BinnedDbn objects.
template<size_t DbnN, typename... AxisT>
BinnedDbn< DbnN, AxisT... >	operator+ (BinnedDbn< DbnN, AxisT... > first, const BinnedDbn< DbnN, AxisT... > &second)
template<size_t DbnN, typename... AxisT>
BinnedDbn< DbnN, AxisT... >	operator- (BinnedDbn< DbnN, AxisT... > first, BinnedDbn< DbnN, AxisT... > &&second)
	Subtract one BinnedDbn object from another.
template<size_t DbnN, typename... AxisT>
BinnedDbn< DbnN, AxisT... >	operator- (BinnedDbn< DbnN, AxisT... > first, const BinnedDbn< DbnN, AxisT... > &second)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	divide (const BinnedDbn< DbnN, AxisT... > &numer, const BinnedDbn< DbnN, AxisT... > &denom)
	Divide two BinnedDbn objects.
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (const BinnedDbn< DbnN, AxisT... > &numer, const BinnedDbn< DbnN, AxisT... > &denom)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (const BinnedDbn< DbnN, AxisT... > &numer, BinnedDbn< DbnN, AxisT... > &&denom)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (BinnedDbn< DbnN, AxisT... > &&numer, const BinnedDbn< DbnN, AxisT... > &denom)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (BinnedDbn< DbnN, AxisT... > &&numer, BinnedDbn< DbnN, AxisT... > &&denom)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	efficiency (const BinnedDbn< DbnN, AxisT... > &accepted, const BinnedDbn< DbnN, AxisT... > &total)
	Calculate a binned efficiency ratio of two BinnedDbn objects.
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	asymm (const BinnedDbn< DbnN, AxisT... > &a, const BinnedDbn< DbnN, AxisT... > &b)
	Calculate the asymmetry (a-b)/(a+b) of two BinnedDbn objects.
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	mkIntegral (const BinnedDbn< DbnN, AxisT... > &histo, const bool includeOverflows=true)
	Convert a BinnedDbn to a BinnedEstimate representing the integral of the histogram.
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	mkIntegralEff (const BinnedDbn< DbnN, AxisT... > &histo, const bool includeOverflows=true)
	Convert a BinnedDbn to a BinnedEstimate where each bin is a fraction of the total.
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	add (const BinnedDbn< DbnN, AxisT... > &dbn, const BinnedEstimate< AxisT... > &est)
	Calculate the addition of a BinnedDbn with a BinnedEstimate.
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator+ (const BinnedDbn< DbnN, AxisT... > &dbn, const BinnedEstimate< AxisT... > &est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator+ (BinnedDbn< DbnN, AxisT... > &&dbn, const BinnedEstimate< AxisT... > &est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator+ (const BinnedDbn< DbnN, AxisT... > &dbn, BinnedEstimate< AxisT... > &&est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator+ (BinnedDbn< DbnN, AxisT... > &&dbn, BinnedEstimate< AxisT... > &&est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	subtract (const BinnedDbn< DbnN, AxisT... > &dbn, const BinnedEstimate< AxisT... > &est)
	Calculate the subtraction of a BinnedEstimate from a BinnedDbn.
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator- (const BinnedDbn< DbnN, AxisT... > &dbn, const BinnedEstimate< AxisT... > &est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator- (BinnedDbn< DbnN, AxisT... > &&dbn, const BinnedEstimate< AxisT... > &est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator- (const BinnedDbn< DbnN, AxisT... > &dbn, BinnedEstimate< AxisT... > &&est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator- (BinnedDbn< DbnN, AxisT... > &&dbn, BinnedEstimate< AxisT... > &&est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	divide (const BinnedDbn< DbnN, AxisT... > &dbn, const BinnedEstimate< AxisT... > &est)
	Calculate the division of a BinnedDbn and a BinnedEstimate.
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (const BinnedDbn< DbnN, AxisT... > &dbn, const BinnedEstimate< AxisT... > &est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (BinnedDbn< DbnN, AxisT... > &&dbn, const BinnedEstimate< AxisT... > &est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (const BinnedDbn< DbnN, AxisT... > &dbn, BinnedEstimate< AxisT... > &&est)
template<size_t DbnN, typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (BinnedDbn< DbnN, AxisT... > &&dbn, BinnedEstimate< AxisT... > &&est)
template<size_t DbnN, typename... AxisT, typename... Args, typename = std::enable_if_t<(DbnN == sizeof...(AxisT)+1 && (std::is_same_v<BinnedDbn<DbnN, AxisT...>, Args> && ...))>>
ScatterND< sizeof...(Args)+1 >	zipProfiles (const BinnedDbn< DbnN, AxisT... > &p1, Args &&... others, const std::string &path="")
	Zip profile objects of the same type into a combined scatter object.
Combining BinnedEstimates: global operators
template<typename... AxisT>
BinnedEstimate< AxisT... >	operator+ (BinnedEstimate< AxisT... > first, const BinnedEstimate< AxisT... > &second)
	Add two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	operator+ (BinnedEstimate< AxisT... > first, BinnedEstimate< AxisT... > &&second)
	Add two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	operator- (BinnedEstimate< AxisT... > first, const BinnedEstimate< AxisT... > &second)
	Subtract two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	operator- (BinnedEstimate< AxisT... > first, BinnedEstimate< AxisT... > &&second)
	Subtract two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	divide (const BinnedEstimate< AxisT... > &numer, const BinnedEstimate< AxisT... > &denom, const std::string &pat_uncorr="^stat|^uncor")
	Divide two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (const BinnedEstimate< AxisT... > &numer, const BinnedEstimate< AxisT... > &denom)
	Divide two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (BinnedEstimate< AxisT... > &&numer, const BinnedEstimate< AxisT... > &denom)
	Divide two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (const BinnedEstimate< AxisT... > &numer, BinnedEstimate< AxisT... > &&denom)
	Divide two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	operator/ (BinnedEstimate< AxisT... > &&numer, BinnedEstimate< AxisT... > &&denom)
	Divide two BinnedEstimates.
template<typename... AxisT>
BinnedEstimate< AxisT... >	efficiency (const BinnedEstimate< AxisT... > &accepted, const BinnedEstimate< AxisT... > &total, const std::string &pat_uncorr="^stat|^uncor")
	Calculate a binned efficiency ratio of two BinnedEstimate objects.
template<typename... AxisT>
BinnedEstimate< AxisT... >	asymm (const BinnedEstimate< AxisT... > &a, const BinnedEstimate< AxisT... > &b, const std::string &pat_uncorr="^stat|^uncor")
	Calculate the asymmetry (a-b)/(a+b) of two BinnedDbn objects.
Generalised transformations
template<typename... AxisT>
void	transform (BinnedEstimate< AxisT... > &est, const Trf< 1 > &fn)
template<typename... AxisT, typename FN >
void	transform (BinnedEstimate< AxisT... > &est, const FN &fn)
void	transform (Estimate0D &est, const Trf< 1 > &fn)
template<typename FN >
void	transform (Estimate0D &est, const FN &fn)
template<size_t N>
void	transform (ScatterND< N > &s, const Trf< N > &fn, const size_t i)
template<size_t N, typename FN >
void	transform (ScatterND< N > &s, const FN &fn, const size_t i)
template<size_t N, typename FN >
void	transformX (ScatterND< N > &s, const FN &fn)
template<size_t N, typename FN >
void	transformY (ScatterND< N > &s, const FN &fn)
template<size_t N, typename FN >
void	transformZ (ScatterND< N > &s, const FN &fn)
Combining counters: global operators
Counter	operator+ (Counter first, const Counter &second)
	Add two counters.
Counter	operator+ (Counter first, Counter &&second)
	Add two counters.
Counter	operator- (Counter first, const Counter &second)
	Subtract two counters.
Counter	operator- (Counter first, Counter &&second)
	Subtract two counters.
Estimate0D	divide (const Counter &numer, const Counter &denom)
	Divide two counters, with an uncorrelated error treatment.
Estimate0D	operator/ (const Counter &numer, const Counter &denom)
	Divide two Counter objects.
Estimate0D	operator/ (Counter &&numer, const Counter &denom)
	Divide two Counter objects.
Estimate0D	operator/ (const Counter &numer, Counter &&denom)
	Divide two Counter objects.
Estimate0D	operator/ (Counter &&numer, Counter &&denom)
	Divide two Counter objects.
Estimate0D	efficiency (const Counter &accepted, const Counter &total)
	Calculate an efficiency ratio of two counters.
Global operators for Estimate objects
Estimate	operator+ (Estimate lhs, const Estimate &rhs)
	Add two Estimate objects.
Estimate	operator+ (Estimate lhs, Estimate &&rhs)
	Add two Estimate objects.
Estimate	operator- (Estimate lhs, const Estimate &rhs)
	Subtract two Estimate objects.
Estimate	operator- (Estimate lhs, Estimate &&rhs)
	Subtract two Estimate objects.
Estimate	divide (const Estimate &numer, const Estimate &denom, const std::string &pat_uncorr="^stat|^uncor")
	Divide two Estimate objects.
Estimate	operator/ (const Estimate &numer, const Estimate &denom)
	Divide two Estimate objects.
Estimate	operator/ (Estimate &&numer, const Estimate &denom)
	Divide two Estimate objects.
Estimate	operator/ (const Estimate &numer, Estimate &&denom)
	Divide two Estimate objects.
Estimate	operator/ (Estimate &&numer, Estimate &&denom)
	Divide two Estimate objects.
Estimate	efficiency (const Estimate &accepted, const Estimate &total, const std::string &pat_uncorr="^stat|^uncor")
	Divide two Estimate objects using binomial statistics.
Global operators for Estimate0D objects
Estimate0D	operator+ (Estimate0D lhs, const Estimate0D &rhs)
	Add two Estimate0D objects.
Estimate0D	operator+ (Estimate0D lhs, Estimate0D &&rhs)
	Add two Estimate0D objects.
Estimate0D	operator- (Estimate0D lhs, const Estimate0D &rhs)
	Subtract two Estimate0D objects.
Estimate0D	operator- (Estimate0D lhs, Estimate0D &&rhs)
	Subtract two Estimate0D objects.
Estimate0D	divide (const Estimate0D &numer, const Estimate0D &denom, const std::string &pat_uncorr="^stat|^uncor")
	Divide two Estimate0D objects.
Estimate0D	operator/ (const Estimate0D &numer, const Estimate0D &denom)
	Divide two Estimate0D objects.
Estimate0D	operator/ (Estimate0D &&numer, const Estimate0D &denom)
	Divide two Estimate0D objects.
Estimate0D	operator/ (const Estimate0D &numer, Estimate0D &&denom)
	Divide two Estimate0D objects.
Estimate0D	operator/ (Estimate0D &&numer, Estimate0D &&denom)
	Divide two Estimate0D objects.
Estimate0D	efficiency (const Estimate0D &accepted, const Estimate0D &total, const std::string &pat_uncorr="^stat|^uncor")
	Divide two Estimate0D objects using binomial statistics.
Writer functions to files (with automatic format detection)
void	write (const std::string &filename, const AnalysisObject &ao, int precision=-1)
	Write out object ao to file filename.
template<typename RANGE >
void	write (const std::string &filename, const RANGE &aos, int precision=-1)
	Write out a collection of objects objs to file filename.
template<typename AOITER >
void	write (const std::string &filename, const AOITER &begin, const AOITER &end, int precision=-1)
Writer functions to streams (with explicit format specification)
void	write (std::ostream &os, const AnalysisObject &ao, const std::string &fmt, int precision=-1)
	Write out object ao to stream os with format fmt.
template<typename RANGE >
void	write (std::ostream &os, const RANGE &aos, const std::string &fmt, int precision=-1)
	Write out a collection of objects objs to file filename.
template<typename AOITER >
void	write (std::ostream &os, const AOITER &begin, const AOITER &end, const std::string &fmt, int precision=-1)
Reader functions from files (with automatic format detection)
void	read (const std::string &filename, std::vector< AnalysisObject * > &aos, const std::string &match="", const std::string &unmatch="")
	Read in a collection of objects objs from file filename.
std::vector< AnalysisObject * >	read (const std::string &filename, const std::string &match="", const std::string &unmatch="")
	Read in a collection of objects from file filename.
Reader functions from streams (with explicit format specification)
void	read (std::istream &is, std::vector< AnalysisObject * > &aos, const std::string &fmt, const std::string &match="", const std::string &unmatch="")
	Read in a collection of objects objs from stream is, expecting format fmt.
std::vector< AnalysisObject * >	read (std::istream &is, const std::string &fmt, const std::string &match="", const std::string &unmatch="")
	Read in a collection of objects from stream is, expecting format fmt.
Comparison operators
template<size_t N>
bool	operator== (const PointBase< N > &a, const PointBase< N > &b)
	Equality test.
template<size_t N>
bool	operator!= (const PointBase< N > &a, const PointBase< N > &b)
	Inequality test.
template<size_t N>
bool	operator< (const PointBase< N > &a, const PointBase< N > &b)
	Less-than operator used to sort points.
template<size_t N>
bool	operator<= (const PointBase< N > &a, const PointBase< N > &b)
	Less-than-or-equals operator used to sort points.
template<size_t N>
bool	operator> (const PointBase< N > &a, const PointBase< N > &b)
	Greater-than operator used to sort points.
template<size_t N>
bool	operator>= (const PointBase< N > &a, const PointBase< N > &b)
	Greater-than-or-equals operator used to sort points.
Combining scatters by merging sets of points
template<int N>
ScatterND< N >	combine (ScatterND< N > a, const ScatterND< N > &b)
template<int N>
ScatterND< N >	combine (ScatterND< N > a, ScatterND< N > &&b)
template<int N>
ScatterND< N >	combine (const std::vector< ScatterND< N > > &scatters)
template<int N>
ScatterND< N >	combine (std::vector< ScatterND< N > > &&scatters)
Helper methods to stringify edge types
template<typename A , typename... As>
std::string	mkAxisConfig ()
	Helper function to construct the axis config.
template<ssize_t DbnN, typename A , typename... As>
std::string	mkTypeString ()
	Helper function to construct the BinnedDbn and BinnedEstimate type names.
template<typename A , typename... As>
std::string	mkTypeString ()
	Same as above, but for non-Dbn bin contents.
Miscellaneous numerical helpers
template<typename NUM >
NUM	sqr (NUM a)
	Named number-type squaring operation.
template<typename... Num>
std::enable_if_t< std::conjunction_v< std::is_arithmetic< Num >... >, double >	add_quad (Num ... vals)
	Named number-type addition in quadrature operation.
int	sign (double val)
	Find the sign of a number.
int	sign (int val)
	Find the sign of a number.
int	sign (long val)
	Find the sign of a number.
double	subtract (double a, double b, double tolerance=1e-5)
	Subtract two numbers with FP fuzziness.
double	add (double a, double b, double tolerance=1e-5)
	Add two numbers with FP fuzziness.
Binning helper functions
std::vector< double >	linspace (size_t nbins, double xmin, double xmax, bool include_end=true)
	Make a list of nbins + 1 values uniformly spaced between xmin and xmax inclusive.
std::vector< double >	logspace (size_t nbins, double xmin, double xmax, bool include_end=true)
	Make a list of nbins + 1 values uniformly spaced in log(x) between xmin and xmax inclusive.
std::vector< double >	pdfspace (size_t nbins, double xmin, double xmax, std::function< double(double)> &fn, size_t nsample=10000)
	Make a list of nbins + 1 values spaced with density ~ f(x) between xmin and end inclusive.
template<typename NUM >
int	index_between (const NUM &val, const std::vector< NUM > &binedges)
	Return the bin index of the given value, val, given a vector of bin edges.
Statistics functions
double	effNumEntries (const double sumW, const double sumW2)
	Calculate the effective number of entries of a sample.
double	effNumEntries (const std::vector< double > &weights)
	Calculate the effective number of entries of a sample.
double	mean (const std::vector< int > &sample)
	Calculate the mean of a sample.
double	mean (const double sumWX, const double sumW)
	Calculate the weighted mean of a sample.
double	mean (const std::vector< double > &sample, const std::vector< double > &weights)
	Calculate the weighted mean of a sample.
double	variance (const double sumWX, const double sumW, const double sumWX2, const double sumW2)
	Calculate the weighted variance of a sample.
double	variance (const std::vector< double > &sample, const std::vector< double > &weights)
	Calculate the weighted variance of a sample.
double	stdDev (const double sumWX, const double sumW, const double sumWX2, const double sumW2)
	Calculate the weighted standard deviation of a sample.
double	stdDev (const std::vector< double > &sample, const std::vector< double > &weights)
	Calculate the weighted variance of a sample.
double	stdErr (const double sumWX, const double sumW, const double sumWX2, const double sumW2)
	Calculate the weighted standard error of a sample.
double	stdErr (const std::vector< double > &sample, const std::vector< double > &weights)
	Calculate the weighted variance of a sample.
double	RMS (const double sumWX2, const double sumW, const double sumW2)
	Calculate the weighted RMS of a sample.
double	RMS (const std::vector< double > &sample, const std::vector< double > &weights)
	Calculate the weighted RMS of a sample.
double	covariance (const std::vector< int > &sample1, const std::vector< int > &sample2)
	Calculate the covariance (variance) between two samples.
double	correlation (const std::vector< int > &sample1, const std::vector< int > &sample2)
	Calculate the correlation strength between two samples.
double	naiveChi2 (const std::vector< double > &sample1, const std::vector< double > &sample2, const std::vector< double > &s1errors=std::vector< double >{}, const std::vector< double > &s2errors=std::vector< double >{})
	Calculate the error-weighted chi2 statistic between two samples.
double	naiveChi2reduced (const std::vector< double > &sample1, const std::vector< double > &sample2, const std::vector< double > &s1errors=std::vector< double >{}, const std::vector< double > &s2errors=std::vector< double >{})
	Calculate the error-weighted reduced chi2 statistic between two samples.
Combining weights: global operators
Weights	operator+ (const Weights &first, const Weights &second)
	Add two weights.
Weights	operator- (const Weights &first, const Weights &second)
	Subtract two weights.
Weights	operator* (const Weights &first, const Weights &second)
	Multiply two weights.
Weights	operator/ (const Weights &numer, const Weights &denom)
	Divide two weights.
Weights	operator* (double a, const Weights &w)
	Multiply by a double.
Weights	operator* (const Weights &w, double a)
	Multiply by a double.
Weights	operator/ (const Weights &w, double a)
	Divide by a double.
Weights	operator/ (double a, const Weights &w)

Variables
const size_t	SEARCH_SIZElc = 16
const size_t	BISECT_LINEAR_THRESHOLDlc = 32
static const double	MAXDOUBLE = DBL_MAX
static const double	MAXINT = INT_MAX
static const double	PI = M_PI
	A pre-defined value of .
static const double	TWOPI = 2*M_PI
	A pre-defined value of .
static const double	HALFPI = M_PI_2
	A pre-defined value of .
template<typename... T>
constexpr bool	isIterable = std::conjunction<Iterable<T>...>::value
template<typename... T>
constexpr bool	isCIterable = std::conjunction<CIterable<T>...>::value
static bool	enableH5compression = Utils::getEnvParam("YODA_HDF5_COMPRESSION", true)
static const size_t	YODA_H5_FORMAT_VERSION = 1
static const int	YODA_FORMAT_VERSION = 3

Ranges and intervals
enum	RangeBoundary { OPEN =0 , SOFT =0 , CLOSED =1 , HARD =1 }
template<typename NUM >
bool	inRange (NUM value, NUM low, NUM high, RangeBoundary lowbound=CLOSED, RangeBoundary highbound=OPEN)
	Determine if value is in the range low to high, for floating point numbers.
template<typename NUM >
bool	inRange (NUM value, std::pair< NUM, NUM > lowhigh, RangeBoundary lowbound=CLOSED, RangeBoundary highbound=OPEN)
	Alternative version of inRange for doubles, which accepts a pair for the range arguments.
bool	inRange (int value, int low, int high, RangeBoundary lowbound=CLOSED, RangeBoundary highbound=CLOSED)
	Determine if value is in the range low to high, for integer types.
bool	inRange (int value, std::pair< int, int > lowhigh, RangeBoundary lowbound=CLOSED, RangeBoundary highbound=OPEN)
	Alternative version of inRange for ints, which accepts a pair for the range arguments.

Comparison functions for safe (floating point) equality tests
static std::function< bool(const double, const double)>	fuzzyEqComp
	Comparator wrapper to use with STL algorithms, e.g. std::equal etc.
template<typename NUM >
std::enable_if_t< std::is_floating_point_v< NUM >, bool >	isZero (NUM val, double tolerance=1e-5)
	Compare a number to zero.
template<typename NUM >
std::enable_if_t< std::is_integral_v< NUM >, bool >	isZero (NUM val, double=1e-5)
	Compare a number to zero.
template<typename NUM >
std::enable_if_t< std::is_floating_point_v< NUM >, bool >	isNaN (NUM val)
	Check if a number is NaN.
template<typename NUM >
std::enable_if_t< std::is_floating_point_v< NUM >, bool >	notNaN (NUM val)
	Check if a number is non-NaN.
template<typename N1 , typename N2 >
std::enable_if_t< std::is_arithmetic_v< N1 > &&std::is_arithmetic_v< N2 > &&(std::is_floating_point_v< N1 >||std::is_floating_point_v< N2 >), bool >	fuzzyEquals (N1 a, N2 b, double tolerance=1e-5)
	Compare two numbers for equality with a degree of fuzziness.
template<typename N1 , typename N2 >
std::enable_if_t< std::is_integral_v< N1 > &&std::is_integral_v< N2 >, bool >	fuzzyEquals (N1 a, N2 b, double)
	Compare two numbers for equality with a degree of fuzziness.
template<typename N1 , typename N2 >
std::enable_if_t< std::is_arithmetic_v< N1 > &&std::is_arithmetic_v< N2 >, bool >	fuzzyGtrEquals (N1 a, N2 b, double tolerance=1e-5)
	Compare two numbers for >= with a degree of fuzziness.
template<typename N1 , typename N2 >
std::enable_if_t< std::is_arithmetic_v< N1 > &&std::is_arithmetic_v< N2 >, bool >	fuzzyLessEquals (N1 a, N2 b, double tolerance=1e-5)
	Compare two floating point numbers for <= with a degree of fuzziness.
double	approx (double a, int n=5)
	Returns a number floored at the nth decimal place.

Detailed Description

Anonymous namespace to limit visibility.

Todo:

Add SFINAE math type stuff (see Rivet) and add inrange() and inrange_closed_closed() etc. aliases cf. MCUtils

Typedef Documentation

all_CAxes

template<typename... EdgeT>

using YODA::all_CAxes = typedef typename std::conjunction<std::is_floating_point<EdgeT>...>

Definition at line 18 of file BinningUtils.h.

AO

using YODA::AO = typedef AnalysisObject

Convenience alias.

Definition at line 376 of file AnalysisObject.h.

BinnedEstimate1D

template<typename A1 >

using YODA::BinnedEstimate1D = typedef BinnedEstimate<A1>

Define dimension-specific short-hands (Cython sugar)

Definition at line 1293 of file BinnedEstimate.h.

BinnedEstimate2D

template<typename A1 , typename A2 >

using YODA::BinnedEstimate2D = typedef BinnedEstimate<A1, A2>

Definition at line 1296 of file BinnedEstimate.h.

BinnedEstimate3D

template<typename A1 , typename A2 , typename A3 >

using YODA::BinnedEstimate3D = typedef BinnedEstimate<A1, A2, A3>

Definition at line 1299 of file BinnedEstimate.h.

BinnedHisto

template<typename... AxisTypes>

using YODA::BinnedHisto = typedef BinnedDbn<sizeof...(AxisTypes), AxisTypes...>

Definition at line 102 of file BinnedDbn.h.

BinnedHisto1D

template<typename A1 >

using YODA::BinnedHisto1D = typedef BinnedHisto<A1>

Define dimension-specific short-hands (Cython sugar)

Definition at line 331 of file Histo.h.

BinnedHisto2D

template<typename A1 , typename A2 >

using YODA::BinnedHisto2D = typedef BinnedHisto<A1, A2>

Definition at line 334 of file Histo.h.

BinnedHisto3D

template<typename A1 , typename A2 , typename A3 >

using YODA::BinnedHisto3D = typedef BinnedHisto<A1, A2, A3>

Definition at line 337 of file Histo.h.

BinnedProfile

template<typename... AxisTypes>

using YODA::BinnedProfile = typedef BinnedDbn<sizeof...(AxisTypes)+1, AxisTypes...>

Definition at line 105 of file BinnedDbn.h.

BinnedProfile1D

template<typename A1 >

using YODA::BinnedProfile1D = typedef BinnedProfile<A1>

Define dimension-specific short-hands (Cython sugar)

Definition at line 326 of file Profile.h.

BinnedProfile2D

template<typename A1 , typename A2 >

using YODA::BinnedProfile2D = typedef BinnedProfile<A1, A2>

Definition at line 329 of file Profile.h.

BinnedProfile3D

template<typename A1 , typename A2 , typename A3 >

using YODA::BinnedProfile3D = typedef BinnedProfile<A1, A2, A3>

Definition at line 332 of file Profile.h.

Dbn0D

using YODA::Dbn0D = typedef Dbn<0>

User-friendly aliases.

Definition at line 775 of file Dbn.h.

Dbn1D

using YODA::Dbn1D = typedef Dbn<1>

Definition at line 776 of file Dbn.h.

Dbn2D

using YODA::Dbn2D = typedef Dbn<2>

Definition at line 777 of file Dbn.h.

Dbn3D

using YODA::Dbn3D = typedef Dbn<3>

Definition at line 778 of file Dbn.h.

EdgeHandlerBasePtr

using YODA::EdgeHandlerBasePtr = typedef typename std::shared_ptr<EdgeHandlerBase>

Definition at line 266 of file H5Utils.h.

EdgeHandlerPtr

template<typename T >

using YODA::EdgeHandlerPtr = typedef typename std::shared_ptr<EdgeHandler<T> >

Convenience aliases.

Definition at line 264 of file H5Utils.h.

enable_if_all_CAxisT

template<typename... EdgeT>

using YODA::enable_if_all_CAxisT = typedef std::enable_if_t<all_CAxes<EdgeT...>::value>

Checks if all edge types are continuous.

Definition at line 22 of file BinningUtils.h.

enable_if_CAxisT

template<typename EdgeT >

using YODA::enable_if_CAxisT = typedef std::enable_if_t<std::is_floating_point<EdgeT>::value, EdgeT>

Checks if edge type is continuous and returns edge type.

Definition at line 26 of file BinningUtils.h.

enable_if_DAxisT

template<typename EdgeT >

using YODA::enable_if_DAxisT = typedef std::enable_if_t<!std::is_floating_point<EdgeT>::value, EdgeT>

Checks if edge type is discrete and returns edge type.

Definition at line 30 of file BinningUtils.h.

Estimate1D

using YODA::Estimate1D = typedef BinnedEstimate<double>

Definition at line 1317 of file BinnedEstimate.h.

Estimate2D

using YODA::Estimate2D = typedef BinnedEstimate<double,double>

Definition at line 1318 of file BinnedEstimate.h.

Estimate3D

using YODA::Estimate3D = typedef BinnedEstimate<double,double,double>

Definition at line 1319 of file BinnedEstimate.h.

EstimateND

template<size_t N>

using YODA::EstimateND = typedef typename EstimateMaker<std::make_index_sequence<N> >::type

Definition at line 1313 of file BinnedEstimate.h.

Histo1D

using YODA::Histo1D = typedef BinnedHisto<double>

User-friendly familiar names (continuous axes only)

Definition at line 354 of file Histo.h.

Histo2D

using YODA::Histo2D = typedef BinnedHisto<double,double>

Definition at line 355 of file Histo.h.

Histo3D

using YODA::Histo3D = typedef BinnedHisto<double,double,double>

Definition at line 356 of file Histo.h.

HistoND

template<size_t N>

using YODA::HistoND = typedef typename HistoMaker<std::make_index_sequence<N> >::type

Definition at line 351 of file Histo.h.

Point1D

using YODA::Point1D = typedef PointND<1>

User-familiar alias.

Definition at line 714 of file Point.h.

Point2D

using YODA::Point2D = typedef PointND<2>

Definition at line 715 of file Point.h.

Point3D

using YODA::Point3D = typedef PointND<3>

Definition at line 716 of file Point.h.

Point4D

using YODA::Point4D = typedef PointND<4>

Definition at line 717 of file Point.h.

Profile1D

using YODA::Profile1D = typedef BinnedProfile<double>

User-friendly familiar names (continuous axes only)

Definition at line 350 of file Profile.h.

Profile2D

using YODA::Profile2D = typedef BinnedProfile<double,double>

Definition at line 351 of file Profile.h.

Profile3D

using YODA::Profile3D = typedef BinnedProfile<double,double,double>

Definition at line 352 of file Profile.h.

ProfileND

template<size_t N>

using YODA::ProfileND = typedef typename ProfileMaker<std::make_index_sequence<N> >::type

User-friendly name for the N-dimensional profile with all-continuous axes.

Definition at line 347 of file Profile.h.

S1D

using YODA::S1D = typedef Scatter1D

Definition at line 905 of file Scatter.h.

S2D

using YODA::S2D = typedef Scatter2D

Definition at line 906 of file Scatter.h.

S3D

using YODA::S3D = typedef Scatter3D

Definition at line 907 of file Scatter.h.

S4D

using YODA::S4D = typedef Scatter4D

Definition at line 908 of file Scatter.h.

Scatter1D

using YODA::Scatter1D = typedef ScatterND<1>

Definition at line 901 of file Scatter.h.

Scatter2D

using YODA::Scatter2D = typedef ScatterND<2>

Definition at line 902 of file Scatter.h.

Scatter3D

using YODA::Scatter3D = typedef ScatterND<3>

Definition at line 903 of file Scatter.h.

Scatter4D

using YODA::Scatter4D = typedef ScatterND<4>

Definition at line 904 of file Scatter.h.

Trf

template<size_t N>

using YODA::Trf = typedef Transformation<N>

Definition at line 126 of file Transformation.h.

Enumeration Type Documentation

RangeBoundary

enum YODA::RangeBoundary

Represents whether an interval is open (non-inclusive) or closed (inclusive).

For example, the interval is closed (an inclusive boundary) at 0, and open (a non-inclusive boundary) at .

Enumerator
OPEN
SOFT
CLOSED
HARD

Definition at line 156 of file MathUtils.h.

{ OPEN=0, SOFT=0, CLOSED=1, HARD=1 };

Sign

enum YODA::Sign

Enum for signs of numbers.

Enumerator
MINUS
ZERO
PLUS

Definition at line 51 of file MathUtils.h.

{ MINUS = -1, ZERO = 0, PLUS = 1 };

Function Documentation

add() [1/2]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::add ( const BinnedDbn< DbnN, AxisT... > &  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Calculate the addition of a BinnedDbn with a BinnedEstimate.

Definition at line 1347 of file BinnedDbn.h.

                                                                                 {
    return dbn.mkEstimate() + est;
  }

References YODA::DbnStorage< DbnN, AxisT >::mkEstimate().

Referenced by asymm(), efficiency(), efficiency(), operator+(), operator+(), operator+(), and operator+().

add() [2/2]

double YODA::add ( double  a, double  b, double  tolerance = 1e-5  )

inline

Add two numbers with FP fuzziness.

Definition at line 253 of file MathUtils.h.

                                                                 {
    return subtract(a,-b,tolerance);
  }

References subtract().

add_quad()

template<typename... Num>

std::enable_if_t< std::conjunction_v< std::is_arithmetic< Num >... >, double > YODA::add_quad ( Num ...  vals )

inline

Named number-type addition in quadrature operation.

Definition at line 223 of file MathUtils.h.

                         {
    return sqrt((0.0 + ... + sqr(vals)));
  }

References sqr().

Referenced by divide().

approx()

double YODA::approx ( double  a, int  n = 5  )

inline

Returns a number floored at the nth decimal place.

Definition at line 140 of file MathUtils.h.

                                            {
    double roundTo = pow(10.0,n);
    a *= roundTo;
    a = floor(a);
    return a/roundTo;
  }

asymm() [1/2]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::asymm ( const BinnedDbn< DbnN, AxisT... > &  a, const BinnedDbn< DbnN, AxisT... > &  b  )

inline

Calculate the asymmetry (a-b)/(a+b) of two BinnedDbn objects.

Definition at line 1278 of file BinnedDbn.h.

                                                                                {
    return (a-b) / (a+b);
  }

asymm() [2/2]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::asymm ( const BinnedEstimate< AxisT... > &  a, const BinnedEstimate< AxisT... > &  b, const std::string &  pat_uncorr = "^stat|^uncor"  )

inline

Calculate the asymmetry (a-b)/(a+b) of two BinnedDbn objects.

Definition at line 1260 of file BinnedEstimate.h.

                                                     {
    return divde(subtract(a-b, pat_uncorr), add(a+b, pat_uncorr), pat_uncorr);
  }

References add(), and subtract().

combine() [1/4]

template<int N>

ScatterND< N > YODA::combine ( const std::vector< ScatterND< N > > &  scatters )

inline

Definition at line 803 of file Scatter.h.

                                                                         {
    ScatterND<N> rtn;
    rtn.combineWith(scatters);
    return rtn;
  }

References YODA::ScatterND< N >::combineWith().

combine() [2/4]

template<int N>

ScatterND< N > YODA::combine ( ScatterND< N >  a, const ScatterND< N > &  b  )

inline

Definition at line 791 of file Scatter.h.

                                                                     {
    a.combineWith(b);
    return a;
  }

References YODA::ScatterND< N >::combineWith().

combine() [3/4]

template<int N>

ScatterND< N > YODA::combine ( ScatterND< N >  a, ScatterND< N > &&  b  )

inline

Definition at line 797 of file Scatter.h.

                                                                {
    a.combineWith(std::move(b));
    return a;
  }

References YODA::ScatterND< N >::combineWith().

combine() [4/4]

template<int N>

ScatterND< N > YODA::combine ( std::vector< ScatterND< N > > &&  scatters )

inline

Definition at line 810 of file Scatter.h.

                                                                    {
    ScatterND<N> rtn;
    rtn.combineWith(std::move(scatters));
    return rtn;
  }

References YODA::ScatterND< N >::combineWith().

containsNan()

template<typename... Args>

bool YODA::containsNan ( const std::tuple< Args... > &  coords )

inline

Checks if a coordinate tuple has a nan.

Definition at line 30 of file Binning.h.

                                                           {
    std::array<size_t, sizeof...(Args)> hasNan{};
    auto checkCoords = [&hasNan, &coords](auto I) {
      using isContinuous = typename std::is_floating_point<typename std::tuple_element_t<I, std::tuple<Args...>>>;
 
      hasNan[I] = size_t(std::isnan(nullifyIfDiscCoord(std::move(std::get<I>(coords)),
                                                       std::integral_constant<bool,
                                                       isContinuous::value>{})));
    };
 
    MetaUtils::staticFor<sizeof...(Args)>(checkCoords);
 
    return std::any_of(hasNan.begin(), hasNan.end(), [ ](const bool i) { return i; } );
  }

References nullifyIfDiscCoord(), and MetaUtils::staticFor().

Referenced by YODA::FillableStorage< FillDim, BinContentT, AxisT >::fill().

correlation()

double YODA::correlation ( const std::vector< int > &  sample1, const std::vector< int > &  sample2  )

inline

Calculate the correlation strength between two samples.

Definition at line 533 of file MathUtils.h.

                                                                                          {
    const double cov = covariance(sample1, sample2);
    const double var1 = covariance(sample1, sample1);
    const double var2 = covariance(sample2, sample2);
    const double correlation = cov/sqrt(var1*var2);
    const double corr_strength = correlation*sqrt(var2/var1);
    return corr_strength;
  }

References correlation(), and covariance().

Referenced by correlation().

covariance()

double YODA::covariance ( const std::vector< int > &  sample1, const std::vector< int > &  sample2  )

inline

Calculate the covariance (variance) between two samples.

Definition at line 518 of file MathUtils.h.

                                                                                         {
    const double mean1 = mean(sample1);
    const double mean2 = mean(sample2);
    const size_t N = sample1.size();
    double cov = 0.0;
    for (size_t i = 0; i < N; i++) {
      const double cov_i = (sample1[i] - mean1)*(sample2[i] - mean2);
      cov += cov_i;
    }
    if (N > 1) return cov/(N-1);
    else return 0.0;
  }

References mean().

Referenced by correlation().

divide() [1/6]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::divide ( const BinnedDbn< DbnN, AxisT... > &  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Calculate the division of a BinnedDbn and a BinnedEstimate.

Definition at line 1411 of file BinnedDbn.h.

                                                                                    {
    return dbn.mkEstimate() / est;
  }

References YODA::DbnStorage< DbnN, AxisT >::mkEstimate().

divide() [2/6]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::divide ( const BinnedDbn< DbnN, AxisT... > &  numer, const BinnedDbn< DbnN, AxisT... > &  denom  )

inline

Divide two BinnedDbn objects.

Definition at line 1174 of file BinnedDbn.h.

                                                                                         {
 
    if (numer != denom) {
      throw BinningError("Arithmetic operation requires compatible binning!");
    }
 
    BinnedEstimate<AxisT...> rtn = numer.mkEstimate();
    if (numer.path() == denom.path())  rtn.setPath(numer.path());
    if (rtn.hasAnnotation("ScaledBy")) rtn.rmAnnotation("ScaledBy");
 
    for (const auto& b_num : numer.bins(true, true)) {
      const size_t idx = b_num.index();
      const auto& b_den = denom.bin(idx);
      double v, e;
      if (isZero(b_den.effNumEntries())) {
        v = std::numeric_limits<double>::quiet_NaN();
        e = std::numeric_limits<double>::quiet_NaN();
      }
      else {
        if constexpr(DbnN > sizeof...(AxisT)) {
          v = b_num.mean(DbnN) / b_den.mean(DbnN);
          const double e_num = isZero(b_num.effNumEntries())? 0 : b_num.relStdErr(DbnN);
          const double e_den = isZero(b_den.effNumEntries())? 0 : b_den.relStdErr(DbnN);
          e = fabs(v) * sqrt(sqr(e_num) + sqr(e_den));
        }
        else {
          v = b_num.sumW() / b_den.sumW();
          const double e_num = isZero(b_num.effNumEntries())? 0 : b_num.relErrW();
          const double e_den = isZero(b_den.effNumEntries())? 0 : b_den.relErrW();
          e = fabs(v) * sqrt(sqr(e_num) + sqr(e_den));
        }
      }
      rtn.bin(idx).set(v, {-e, e}); // @todo put "stats" as source?
    }
    rtn.maskBins(denom.maskedBins(), true);
 
    return rtn;
  }

References YODA::BinnedStorage< BinContentT, AxisT >::bin(), YODA::BinnedStorage< BinContentT, AxisT >::bins(), isZero(), YODA::BinnedStorage< BinContentT, AxisT >::maskedBins(), YODA::DbnStorage< DbnN, AxisT >::mkEstimate(), YODA::AnalysisObject::path(), and sqr().

Referenced by divide(), divide(), efficiency(), efficiency(), efficiency(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), operator/(), and operator/().

divide() [3/6]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::divide ( const BinnedEstimate< AxisT... > &  numer, const BinnedEstimate< AxisT... > &  denom, const std::string &  pat_uncorr = "^stat|^uncor"  )

inline

Divide two BinnedEstimates.

Definition at line 1180 of file BinnedEstimate.h.

                                                      {
    if (numer != denom) {
      throw BinningError("Arithmetic operation requires compatible binning!");
    }
 
    BinnedEstimate<AxisT...> rtn(numer.binning());
    if (numer.path() == denom.path())  rtn.setPath(numer.path());
    if (rtn.hasAnnotation("ScaledBy")) rtn.rmAnnotation("ScaledBy");
 
    for (const auto& b_num : numer.bins(true, true)) {
      const size_t idx = b_num.index();
      rtn.bin(idx) = divide(b_num, denom.bin(idx), pat_uncorr);
    }
    rtn.maskBins(denom.maskedBins(), true);
 
    return rtn;
  }

References YODA::BinnedStorage< BinContentT, AxisT >::bin(), YODA::BinnedStorage< BinContentT, AxisT >::binning(), YODA::BinnedStorage< BinContentT, AxisT >::bins(), divide(), YODA::BinnedStorage< BinContentT, AxisT >::maskedBins(), and YODA::AnalysisObject::path().

divide() [4/6]

Estimate0D YODA::divide	(	const Counter &	numer,
		const Counter &	denom
	)

Divide two counters, with an uncorrelated error treatment.

Todo:

Add skipnullpts extra optional arg

Definition at line 19 of file Counter.cc.

                                                                {
    Estimate0D rtn;
    if (numer.path() == denom.path())  rtn.setPath(numer.path());
    if (rtn.hasAnnotation("ScaledBy")) rtn.rmAnnotation("ScaledBy");
    if (denom.val() != 0) {
      const double val = numer.val() / denom.val();
      const double err = val * add_quad(numer.relErr(), denom.relErr());
      rtn.set(val, {-err, err});
    }
    return rtn;
  }

References add_quad(), YODA::AnalysisObject::hasAnnotation(), YODA::AnalysisObject::path(), YODA::Counter::relErr(), YODA::AnalysisObject::rmAnnotation(), YODA::Estimate::set(), YODA::AnalysisObject::setPath(), and YODA::Counter::val().

divide() [5/6]

Estimate YODA::divide ( const Estimate &  numer, const Estimate &  denom, const std::string &  pat_uncorr = "^stat|^uncor"  )

inline

Divide two Estimate objects.

Definition at line 684 of file Estimate.h.

                                                                     {
 
    Estimate rtn;
    if (denom.val())  rtn.setVal(numer.val() / denom.val());
    const double newVal = rtn.val();
 
    // get error sources
    std::vector<std::string> sources = numer.sources();
    std::vector<std::string> tmp = denom.sources();
    sources.insert(std::end(sources),
                   std::make_move_iterator(std::begin(tmp)),
                   std::make_move_iterator(std::end(tmp)));
    std::sort(sources.begin(), sources.end());
    sources.erase( std::unique(sources.begin(), sources.end()), sources.end() );
 
    std::smatch match;
    const std::regex re(pat_uncorr, std::regex_constants::icase);
    for (const std::string& src : sources) {
      if (std::regex_search(src, match, re)) {
        // treat as uncorrelated between AOs:
        // add relative errors in quadrature
        double n_dn = 0.0, n_up = 0.0;
        if (numer.hasSource(src)) {
          n_dn = numer.relErrDown(src);
          n_up = numer.relErrUp(src);
        }
        double d_dn = 0.0, d_up = 0.0;
        if (denom.hasSource(src)) {
          d_dn = denom.relErrDown(src);
          d_up = denom.relErrUp(src);
        }
        const double new_dn = fabs(newVal) * std::sqrt(n_dn*n_dn + d_dn*d_dn);
        const double new_up = fabs(newVal) * std::sqrt(n_up*n_up + d_up*d_up);
        rtn.setErr({-new_dn,new_up}, src);
      }
      else {
        // treat as correlated between AOs:
        // work out correlated ratio: R+dR = (N+dN)/(D+dD)
        double n_dn = numer.val(), n_up = numer.val();
        if (numer.hasSource(src)) {
          n_dn += numer.errDown(src);
          n_up += numer.errUp(src);
        }
        double d_dn = denom.val(), d_up = denom.val();
        if (denom.hasSource(src)) {
          d_dn += denom.errDown(src);
          d_up += denom.errUp(src);
        }
        double new_dn = std::numeric_limits<double>::quiet_NaN();
        double new_up = std::numeric_limits<double>::quiet_NaN();
        if (d_dn)  new_dn = n_dn / d_dn - newVal;
        if (d_up)  new_up = n_up / d_up - newVal;
        rtn.setErr({new_dn, new_up}, src);
      }
    }
 
    return rtn;
  }

References YODA::Estimate::errDown(), YODA::Estimate::errUp(), YODA::Estimate::hasSource(), YODA::Estimate::relErrDown(), YODA::Estimate::relErrUp(), YODA::Estimate::setErr(), YODA::Estimate::setVal(), YODA::Estimate::sources(), and YODA::Estimate::val().

divide() [6/6]

Estimate0D YODA::divide ( const Estimate0D &  numer, const Estimate0D &  denom, const std::string &  pat_uncorr = "^stat|^uncor"  )

inline

Divide two Estimate0D objects.

Definition at line 368 of file Estimate0D.h.

                                                                        {
    Estimate0D rtn = divide(static_cast<const Estimate&>(numer),
                            static_cast<const Estimate&>(denom), pat_uncorr);
    if (rtn.hasAnnotation("ScaledBy")) rtn.rmAnnotation("ScaledBy");
    if (numer.path() == denom.path())  rtn.setPath(numer.path());
    return rtn;
  }

References divide(), YODA::AnalysisObject::hasAnnotation(), YODA::AnalysisObject::path(), YODA::AnalysisObject::rmAnnotation(), and YODA::AnalysisObject::setPath().

efficiency() [1/5]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::efficiency ( const BinnedDbn< DbnN, AxisT... > &  accepted, const BinnedDbn< DbnN, AxisT... > &  total  )

inline

Calculate a binned efficiency ratio of two BinnedDbn objects.

Note

An efficiency is not the same thing as a standard division of two BinnedDbn objects: the errors are treated as correlated via binomial statistics.

Note

Neither effNumEntries nor sumW are guaranteed to satisfy num <= den for general weights!

Definition at line 1244 of file BinnedDbn.h.

                                                                                                {
 
    if (accepted != total) {
      throw BinningError("Arithmetic operation requires compatible binning!");
    }
 
    BinnedEstimate<AxisT...> rtn = divide(accepted, total);
 
    for (const auto& b_acc : accepted.bins(true, true)) {
      const auto& b_tot = total.bin(b_acc.index());
      auto& b_rtn = rtn.bin(b_acc.index());
 
      // Check that the numerator is consistent with being a subset of the denominator
      if (b_acc.numEntries() > b_tot.numEntries())
        throw UserError("Attempt to calculate an efficiency when the numerator is not a subset of the denominator: "
                        + Utils::toStr(b_acc.numEntries()) + " entries / " + Utils::toStr(b_tot.numEntries()) + " entries");
 
      // If no entries on the denominator, set eff = err = 0 and move to the next bin
      double eff = std::numeric_limits<double>::quiet_NaN();
      double err = std::numeric_limits<double>::quiet_NaN();
      if (!isZero(b_tot.effNumEntries())) {
        eff = b_rtn.val();
        err = sqrt(fabs( add((1.0-2.0*eff)*b_acc.sumW2(), sqr(eff)*b_tot.sumW2()) / sqr(b_tot.sumW()) ));
      }
      b_rtn.setErr({-err, err}); // @todo put "stats" as source?
    }
    return rtn;
  }

References add(), YODA::BinnedStorage< BinContentT, AxisT >::bin(), YODA::BinnedStorage< BinContentT, AxisT >::bins(), divide(), isZero(), and sqr().

Referenced by efficiency(), and efficiency().

efficiency() [2/5]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::efficiency ( const BinnedEstimate< AxisT... > &  accepted, const BinnedEstimate< AxisT... > &  total, const std::string &  pat_uncorr = "^stat|^uncor"  )

inline

Calculate a binned efficiency ratio of two BinnedEstimate objects.

Note

An efficiency is not the same thing as a standard division of two BinnedEstimate objects: the errors are treated as correlated via binomial statistics.

Definition at line 1234 of file BinnedEstimate.h.

                                                          {
 
    if (accepted != total) {
      throw BinningError("Arithmetic operation requires compatible binning!");
    }
 
    BinnedEstimate<AxisT...> rtn(accepted.binning());
 
    for (const auto& b_acc : accepted.bins(true, true)) {
      Estimate est;
      const size_t idx = b_acc.index();
      try {
        est = efficiency(b_acc, total.bin(idx), pat_uncorr);
      } catch (const UserError& e) {
        //
      }
      rtn.bin(idx).set(est);
    }
    return rtn;
  }

References YODA::BinnedStorage< BinContentT, AxisT >::bin(), YODA::BinnedStorage< BinContentT, AxisT >::binning(), YODA::BinnedStorage< BinContentT, AxisT >::bins(), and efficiency().

efficiency() [3/5]

Estimate0D YODA::efficiency	(	const Counter &	accepted,
		const Counter &	total
	)

Calculate an efficiency ratio of two counters.

Todo:

Add divide functions/operators on pointers

Note that an efficiency is not the same thing as a standard division of two histograms: the errors must be treated as correlated

Todo:

Add skipnullpts extra optional arg

Todo:

Provide optional alt behaviours to fill with NaN or remove the invalid point, or...

Todo:

Todo:

Or throw a LowStatsError exception if h.effNumEntries() (or sumW()?) == 0?

Todo:

Provide optional alt behaviours to fill with NaN or remove the invalid point, or...

Todo:

Todo:

Or throw a LowStatsError exception if h.effNumEntries() (or sumW()?) == 0?

Definition at line 34 of file Counter.cc.

                                                                       {
    Estimate0D tmp = divide(accepted, total);
 
    // Check that the numerator is consistent with being a subset of the denominator (NOT effNumEntries here!)
    if (accepted.numEntries() > total.numEntries() || accepted.sumW() > total.sumW())
      throw UserError("Attempt to calculate an efficiency when the numerator is not a subset of the denominator");
 
    // If no entries on the denominator, set eff = err = 0 and move to the next bin
    double eff = std::numeric_limits<double>::quiet_NaN();
    double err = std::numeric_limits<double>::quiet_NaN();
    if (total.sumW() != 0) {
      eff = accepted.sumW() / total.sumW(); //< Actually this is already calculated by the division...
      err = sqrt(abs( ((1-2*eff)*accepted.sumW2() + sqr(eff)*total.sumW2()) / sqr(total.sumW()) ));
    }
 
    tmp.set(eff, {-err, err});
    return tmp;
  }

References divide(), YODA::Counter::numEntries(), YODA::Estimate::set(), sqr(), YODA::Counter::sumW(), and YODA::Counter::sumW2().

efficiency() [4/5]

Estimate YODA::efficiency ( const Estimate &  accepted, const Estimate &  total, const std::string &  pat_uncorr = "^stat|^uncor"  )

inline

Divide two Estimate objects using binomial statistics.

Check that the numerator is consistent with being a subset of the denominator

Todo:

Need to check that bins are all positive? Integral could be zero due to large +ve/-ve in different bins :O

Definition at line 765 of file Estimate.h.

                                                                         {
 
    const double acc_val = accepted.val();
    const double tot_val = total.val();
    if (acc_val > tot_val)
      throw UserError("Attempt to calculate an efficiency when the numerator is not a subset of the denominator: "
                      + Utils::toStr(acc_val) + " / " + Utils::toStr(tot_val));
 
    Estimate rtn = divide(accepted, total, pat_uncorr);
 
    // get error sources
    std::vector<std::string> sources = accepted.sources();
    std::vector<std::string> tmp = total.sources();
    sources.insert(std::end(sources),
                   std::make_move_iterator(std::begin(tmp)),
                   std::make_move_iterator(std::end(tmp)));
    std::sort(sources.begin(), sources.end());
    sources.erase( std::unique(sources.begin(), sources.end()), sources.end() );
 
    // set binomial error for uncorrelated error sources
    std::smatch match;
    const double eff = rtn.val();
    const std::regex re(pat_uncorr, std::regex_constants::icase);
    for (const std::string& src : sources) {
      double err = std::numeric_limits<double>::quiet_NaN();
      if (!tot_val) {
        rtn.setErr({-err,err}, src);
        continue;
      }
      else if (std::regex_search(src, match, re)) {
        const double acc_err = accepted.relTotalErrAvg();
        const double tot_err = total.totalErrAvg();
        err = sqrt(std::abs( add((1.0-2.0*eff)*sqr(acc_err), sqr(eff)*sqr(tot_err)) / sqr(tot_val) ));
        rtn.setErr({-err,err}, src);
        continue;
      }
    }
 
    return rtn;
  }

References add(), divide(), YODA::Estimate::relTotalErrAvg(), YODA::Estimate::setErr(), YODA::Estimate::sources(), sqr(), YODA::Estimate::totalErrAvg(), and YODA::Estimate::val().

efficiency() [5/5]

Estimate0D YODA::efficiency ( const Estimate0D &  accepted, const Estimate0D &  total, const std::string &  pat_uncorr = "^stat|^uncor"  )

inline

Divide two Estimate0D objects using binomial statistics.

Definition at line 398 of file Estimate0D.h.

                                                                            {
    Estimate0D rtn = efficiency(static_cast<const Estimate&>(accepted),
                                static_cast<const Estimate&>(total), pat_uncorr);
    if (rtn.hasAnnotation("ScaledBy")) rtn.rmAnnotation("ScaledBy");
    if (accepted.path() == total.path())  rtn.setPath(total.path());
    return rtn;
  }

References efficiency(), YODA::AnalysisObject::hasAnnotation(), YODA::AnalysisObject::path(), YODA::AnalysisObject::rmAnnotation(), and YODA::AnalysisObject::setPath().

effNumEntries() [1/2]

double YODA::effNumEntries ( const double  sumW, const double  sumW2  )

inline

Calculate the effective number of entries of a sample.

Definition at line 381 of file MathUtils.h.

                                                                     {
    if (isZero(sumW2))  return 0;
    return sqr(sumW) / sumW2;
  }

References isZero(), and sqr().

Referenced by effNumEntries(), YODA::DbnBase< N >::relErrW(), YODA::DbnBase< N >::relStdErr(), RMS(), stdErr(), stdErr(), and variance().

effNumEntries() [2/2]

double YODA::effNumEntries ( const std::vector< double > &  weights )

inline

Calculate the effective number of entries of a sample.

Definition at line 387 of file MathUtils.h.

                                                                {
    double sumW = 0.0, sumW2 = 0.0;
    for (size_t i = 0; i < weights.size(); ++i) {
      sumW += weights[i];
      sumW2 += sqr(weights[i]);
    }
    return effNumEntries(sumW, sumW2);
  }

References effNumEntries(), and sqr().

fuzzyEquals() [1/2]

template<typename N1 , typename N2 >

std::enable_if_t< std::is_arithmetic_v< N1 > &&std::is_arithmetic_v< N2 > &&(std::is_floating_point_v< N1 >||std::is_floating_point_v< N2 >), bool > YODA::fuzzyEquals ( N1  a, N2  b, double  tolerance = 1e-5  )

inline

Compare two numbers for equality with a degree of fuzziness.

This version for floating point types (if any argument is FP) has a degree of fuzziness expressed by the fractional tolerance parameter, for floating point safety.

Definition at line 96 of file MathUtils.h.

                                                 {
    const double absavg = (std::abs(a) + std::abs(b))/2.0;
    const double absdiff = std::abs(a - b);
    const bool rtn = (isZero(a) && isZero(b)) || absdiff < tolerance*absavg;
    return rtn;
  }

References isZero().

Referenced by YODA::Axis< T, isCAxis< T > >::Axis(), fuzzyGtrEquals(), fuzzyLessEquals(), YODA::Axis< T, isCAxis< T > >::hasSameEdges(), operator==(), and subtract().

fuzzyEquals() [2/2]

template<typename N1 , typename N2 >

std::enable_if_t< std::is_integral_v< N1 > &&std::is_integral_v< N2 >, bool > YODA::fuzzyEquals ( N1  a, N2  b, double    )

inline

Compare two numbers for equality with a degree of fuzziness.

Simpler SFINAE template specialisation for integers, since there is no FP precision issue.

Definition at line 110 of file MathUtils.h.

                                    { //< NB. unused tolerance parameter for ints, still needs a default value!
    return a == b;
  }

fuzzyGtrEquals()

template<typename N1 , typename N2 >

std::enable_if_t< std::is_arithmetic_v< N1 > &&std::is_arithmetic_v< N2 >, bool > YODA::fuzzyGtrEquals ( N1  a, N2  b, double  tolerance = 1e-5  )

inline

Compare two numbers for >= with a degree of fuzziness.

The tolerance parameter on the equality test is as for fuzzyEquals.

Definition at line 125 of file MathUtils.h.

                                                    {
    return a > b || fuzzyEquals(a, b, tolerance);
  }

References fuzzyEquals().

Referenced by YODA::Axis< T, isCAxis< T > >::Axis().

fuzzyLessEquals()

template<typename N1 , typename N2 >

std::enable_if_t< std::is_arithmetic_v< N1 > &&std::is_arithmetic_v< N2 >, bool > YODA::fuzzyLessEquals ( N1  a, N2  b, double  tolerance = 1e-5  )

inline

Compare two floating point numbers for <= with a degree of fuzziness.

The tolerance parameter on the equality test is as for fuzzyEquals.

Definition at line 135 of file MathUtils.h.

                                                     {
    return a < b || fuzzyEquals(a, b, tolerance);
  }

References fuzzyEquals().

Referenced by variance().

getDataPath()

string YODA::getDataPath

(

)

Get the path to the installed share/YODA/ data directory.

Definition at line 26 of file Paths.cc.

                       {
    BrInitError error;
    br_init_lib(&error);
    char* temp = br_find_data_dir(DEFAULTDATADIR);
    const string sharedir(temp);
    free(temp);
    return sharedir + "/YODA";
  }

References br_find_data_dir, and br_init_lib.

Referenced by getYodaDataPath().

getLibPath()

string YODA::getLibPath

(

)

Get the path to the directory containing libYODA.

Definition at line 17 of file Paths.cc.

                      {
    BrInitError error;
    br_init_lib(&error);
    char* temp = br_find_lib_dir(DEFAULTLIBDIR);
    const string libdir(temp);
    free(temp);
    return libdir;
  }

References br_find_lib_dir, and br_init_lib.

getYodaDataPath()

vector< string > YODA::getYodaDataPath

(

)

YODA data paths.

Definition at line 35 of file Paths.cc.

                                   {
    vector<string> dirs;
    // Use the YODA data path variable if set...
    const char* env = getenv("YODA_DATA_PATH");
    if (env) dirs = Utils::pathsplit(env);
    // ... then, unless the path ends in :: ...
    if (!env || strlen(env) < 2 || string(env).substr(strlen(env)-2) != "::") {
      // ... fall back to the YODA data install path
      dirs.push_back(getDataPath());
    }
    return dirs;
  }

References getDataPath().

H5DataSet() [1/2]

template<typename T >

YODA_H5::DataSet YODA::H5DataSet	(	YODA_H5::File &	h5file,
		const string &	label,
		size_t	nrows,
		size_t	chunksize,
		bool	compress
	)

Helper method to construct an empty YODA_H5::DataSet.

Note

This version is suited best for 2D vectors that to be committed row-by-row

Definition at line 52 of file H5Utils.h.

                                                                             {
 
    YODA_H5::DataSetCreateProps props;
    if (compress) { // enable compression
      props.add(YODA_H5::Chunking(vector<hsize_t>{1,chunksize}));
      props.add(YODA_H5::Deflate(9));
    }
    // create the dataset
    return h5file.createDataSet(label, YODA_H5::DataSpace({nrows,chunksize}),
                                YODA_H5::create_datatype<T>(), props);
  }

H5DataSet() [2/2]

template<typename T >

YODA_H5::DataSet YODA::H5DataSet	(	YODA_H5::File &	h5file,
		const string &	label,
		vector< T > &&	data,
		bool	compress
	)

Helper method to construct and fill a YODA_H5::DataSet.

Note

This version is suited best for 1D vectors that to be committed in one go

Definition at line 35 of file H5Utils.h.

                                                               {
 
    YODA_H5::DataSetCreateProps props;
    if (compress && data.size()) {
      props.add(YODA_H5::Chunking(vector<hsize_t>{data.size()}));
      props.add(YODA_H5::Deflate(9));
    }
    return h5file.createDataSet(label, std::move(data), props);
  }

Referenced by YODA::WriterH5::writeAOS(), and YODA::EdgeHandler< T >::writeToFile().

index_between()

template<typename NUM >

int YODA::index_between ( const NUM &  val, const std::vector< NUM > &  binedges  )

inline

Return the bin index of the given value, val, given a vector of bin edges.

NB. The binedges vector must be sorted

Definition at line 361 of file MathUtils.h.

                                                                           {
    if (!inRange(val, binedges.front(), binedges.back())) return -1; //< Out of histo range
    int index = -1;
    for (size_t i = 1; i < binedges.size(); ++i) {
      if (val < binedges[i]) {
        index = i-1;
        break;
      }
    }
    assert(inRange(index, -1, binedges.size()-1));
    return index;
  }

References inRange().

inRange() [1/4]

bool YODA::inRange ( int  value, int  low, int  high, RangeBoundary  lowbound = CLOSED, RangeBoundary  highbound = CLOSED  )

inline

Determine if value is in the range low to high, for integer types.

Interval boundary types are defined by lowbound and highbound.

Todo:

Optimise to one-line at compile time?

Definition at line 189 of file MathUtils.h.

                                                                                     {
    if (lowbound == OPEN && highbound == OPEN) {
      return (value > low && value < high);
    } else if (lowbound == OPEN && highbound == CLOSED) {
      return (value > low && value <= high);
    } else if (lowbound == CLOSED && highbound == OPEN) {
      return (value >= low && value < high);
    } else { // if (lowbound == CLOSED && highbound == CLOSED) {
      return (value >= low && value <= high);
    }
  }

References CLOSED, and OPEN.

inRange() [2/4]

bool YODA::inRange ( int  value, std::pair< int, int >  lowhigh, RangeBoundary  lowbound = CLOSED, RangeBoundary  highbound = OPEN  )

inline

Alternative version of inRange for ints, which accepts a pair for the range arguments.

Definition at line 203 of file MathUtils.h.

                                                                                   {
    return inRange(value, lowhigh.first, lowhigh.second, lowbound, highbound);
  }

References inRange().

inRange() [3/4]

template<typename NUM >

bool YODA::inRange ( NUM  value, NUM  low, NUM  high, RangeBoundary  lowbound = CLOSED, RangeBoundary  highbound = OPEN  )

inline

Determine if value is in the range low to high, for floating point numbers.

Interval boundary types are defined by lowbound and highbound.

Todo:

Optimise to one-line at compile time?

Definition at line 164 of file MathUtils.h.

                                                                                   {
    if (lowbound == OPEN && highbound == OPEN) {
      return (value > low && value < high);
    } else if (lowbound == OPEN && highbound == CLOSED) {
      return (value > low && value <= high);
    } else if (lowbound == CLOSED && highbound == OPEN) {
      return (value >= low && value < high);
    } else { // if (lowbound == CLOSED && highbound == CLOSED) {
      return (value >= low && value <= high);
    }
  }

References CLOSED, and OPEN.

Referenced by index_between(), inRange(), and inRange().

inRange() [4/4]

template<typename NUM >

bool YODA::inRange ( NUM  value, std::pair< NUM, NUM >  lowhigh, RangeBoundary  lowbound = CLOSED, RangeBoundary  highbound = OPEN  )

inline

Alternative version of inRange for doubles, which accepts a pair for the range arguments.

Definition at line 179 of file MathUtils.h.

                                                                                   {
    return inRange(value, lowhigh.first, lowhigh.second, lowbound, highbound);
  }

References inRange().

isNaN()

template<typename NUM >

std::enable_if_t< std::is_floating_point_v< NUM >, bool > YODA::isNaN ( NUM  val )

inline

Check if a number is NaN.

Definition at line 80 of file MathUtils.h.

{ return std::isnan(val); }

isZero() [1/2]

template<typename NUM >

std::enable_if_t< std::is_floating_point_v< NUM >, bool > YODA::isZero ( NUM  val, double  tolerance = 1e-5  )

inline

Compare a number to zero.

This version for floating point types has a degree of fuzziness expressed by the absolute tolerance parameter, for floating point safety.

Definition at line 63 of file MathUtils.h.

                                         {
    return fabs(val) < tolerance;
  }

Referenced by divide(), efficiency(), effNumEntries(), fuzzyEquals(), and sign().

isZero() [2/2]

template<typename NUM >

std::enable_if_t< std::is_integral_v< NUM >, bool > YODA::isZero ( NUM  val, double  = 1e-5  )

inline

Compare a number to zero.

SFINAE template specialisation for integers, since there is no FP precision issue.

Definition at line 73 of file MathUtils.h.

                                 {
    return val==0;
  }

linspace()

std::vector< double > YODA::linspace ( size_t  nbins, double  xmin, double  xmax, bool  include_end = true  )

inline

Make a list of nbins + 1 values uniformly spaced between xmin and xmax inclusive.

Note

The arg ordering and the meaning of the nbins variable is "histogram-like", as opposed to the Numpy/Matlab version.

Definition at line 267 of file MathUtils.h.

                                                                                                   {
    if (xmax < xmin)  throw RangeError("xmax should not be smaller than xmin!");
    if (nbins == 0)   throw RangeError("Requested number of bins is 0!");
    std::vector<double> rtn;
    const double interval = (xmax-xmin)/static_cast<double>(nbins);
    for (size_t i = 0; i < nbins; ++i) {
      rtn.push_back(xmin + i*interval);
    }
    assert(rtn.size() == nbins);
    if (include_end) rtn.push_back(xmax); // exact xmax, not result of n * interval
    return rtn;
  }

Referenced by logspace(), and pdfspace().

logspace()

std::vector< double > YODA::logspace ( size_t  nbins, double  xmin, double  xmax, bool  include_end = true  )

inline

Make a list of nbins + 1 values uniformly spaced in log(x) between xmin and xmax inclusive.

Note

The arg ordering and the meaning of the nbins variable is "histogram-like", as opposed to the Numpy/Matlab version, and the xmin and xmax arguments are expressed in "normal" space, rather than as the logarithms of the xmin/xmax values as in Numpy/Matlab.

Definition at line 286 of file MathUtils.h.

                                                                                                   {
    if (xmax < xmin)  throw RangeError("xmax should not be smaller than xmin!");
    if (xmin < 0)     throw RangeError("xmin should not be negative!");
    if (nbins == 0)   throw RangeError("Requested number of bins is 0!");
    const double logxmin = std::log(xmin);
    const double logxmax = std::log(xmax);
    const std::vector<double> logvals = linspace(nbins, logxmin, logxmax);
    assert(logvals.size() == nbins+1);
    std::vector<double> rtn; rtn.reserve(logvals.size());
    rtn.push_back(xmin);
    for (size_t i = 1; i < logvals.size()-1; ++i) {
      rtn.push_back(std::exp(logvals[i]));
    }
    assert(rtn.size() == nbins);
    if (include_end) rtn.push_back(xmax);
    return rtn;
  }

References linspace().

mean() [1/3]

double YODA::mean ( const double  sumWX, const double  sumW  )

inline

Calculate the weighted mean of a sample.

Definition at line 406 of file MathUtils.h.

                                                            {
    return sumW? sumWX / sumW : std::numeric_limits<double>::quiet_NaN();
  }

mean() [2/3]

double YODA::mean ( const std::vector< double > &  sample, const std::vector< double > &  weights  )

inline

Calculate the weighted mean of a sample.

Definition at line 411 of file MathUtils.h.

                                                       {
    if (sample.size() != weights.size())  throw RangeError("Inputs should have equal length!");
    double sumWX = 0., sumW = 0.;
    for (size_t i = 0; i < sample.size(); ++i) {
      sumW  += weights[i];
      sumWX += weights[i]*sample[i];
    }
    return mean(sumWX, sumW);
  }

References mean().

mean() [3/3]

double YODA::mean ( const std::vector< int > &  sample )

inline

Calculate the mean of a sample.

Definition at line 397 of file MathUtils.h.

                                                   {
    double mean = 0.0;
    for (size_t i=0; i<sample.size(); ++i) {
      mean += sample[i];
    }
    return mean/sample.size();
  }

References mean().

Referenced by covariance(), YODA::DbnBase< N >::mean(), mean(), mean(), YODA::DbnBase< N >::relStdErr(), YODA::XDbnMixin< Derived >::xMean(), YODA::XStatsMixin< Derived >::xMean(), YODA::YDbnMixin< Derived >::yMean(), YODA::YStatsMixin< Derived >::yMean(), zipProfiles(), YODA::ZDbnMixin< Derived >::zMean(), and YODA::ZStatsMixin< Derived >::zMean().

mkAxisConfig()

template<typename A , typename... As>

std::string YODA::mkAxisConfig

(

)

Helper function to construct the axis config.

Definition at line 58 of file BinningUtils.h.

                           {
    return (std::string(TypeID<A>::name()) + ... + TypeID<As>::name());
  }

mkIntegral()

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::mkIntegral ( const BinnedDbn< DbnN, AxisT... > &  histo, const bool  includeOverflows = true  )

inline

Convert a BinnedDbn to a BinnedEstimate representing the integral of the histogram.

Note

The integral histo errors are calculated as sqrt(binvalue), as if they are uncorrelated. This is not in general true for integral histograms, so if you need accurate errors you should explicitly monitor bin-to-bin correlations.

The includeunderflow param chooses whether the underflow bin is included in the integral numbers as an offset.

Definition at line 1293 of file BinnedDbn.h.

                                                                                         {
 
    BinnedEstimate<AxisT...> rtn = histo.mkEstimate();
 
    double sumW = 0.0, sumW2 = 0.0;
    for (const auto& b : histo.bins(includeOverflows)) {
      sumW  += b.sumW();
      sumW2 += b.sumW2();
      const double e = sqrt(sumW2);
      rtn.bin(b.index()).set(sumW, {-e, e});
    }
 
    return rtn;
  }

References YODA::BinnedStorage< BinContentT, AxisT >::bins(), and YODA::DbnStorage< DbnN, AxisT >::mkEstimate().

Referenced by mkIntegralEff().

mkIntegralEff()

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::mkIntegralEff ( const BinnedDbn< DbnN, AxisT... > &  histo, const bool  includeOverflows = true  )

inline

Convert a BinnedDbn to a BinnedEstimate where each bin is a fraction of the total.

Note

This sounds weird: let's explain a bit more! Sometimes we want to take a histo h, make an integral histogram H from it, and then divide H by the total integral of h, such that every bin in H represents the cumulative efficiency of that bin as a fraction of the total. I.e. an integral histo, scaled by 1/total_integral and with binomial errors.

The includeunderflow param behaves as for toIntegral, and applies to both the initial integration and the integral used for the scaling. The includeoverflow param applies only to obtaining the scaling factor.

Todo:

Or throw a LowStatsError exception if h.effNumEntries() == 0?

Todo:

Todo:

Provide optional alt behaviours

Todo:

Todo:

Need to check that bins are all positive? Integral could be zero due to large +ve/-ve in different bins :O

Definition at line 1322 of file BinnedDbn.h.

                                                                                            {
 
    BinnedEstimate<AxisT...> rtn = mkIntegral(histo, includeOverflows);
    const double integral = histo.integral(includeOverflows);
 
    // If the integral is empty, the (integrated) efficiency values may as well all be zero, so return here
    if (!integral) return rtn;
 
    const double integral_err = histo.integralError(includeOverflows);
    for (const auto& b : rtn.bins(includeOverflows)) {
      const double eff = b.val() / integral;
      const double err = sqrt(std::abs( ((1-2*eff)*sqr(b.relTotalErrAvg()) + sqr(eff)*sqr(integral_err)) / sqr(integral) ));
      b.set(eff, {-err,err});
    }
 
    return rtn;
  }

References YODA::DbnStorage< DbnN, AxisT >::integral(), YODA::DbnStorage< DbnN, AxisT >::integralError(), mkIntegral(), and sqr().

mkReader()

Reader & YODA::mkReader

(

const std::string &

format_name

)

Factory function to make a reader object by format name or a filename.

<

Todo:

Improve/remove... .ydat?

<

Todo:

Improve/remove... .ydat?

Definition at line 19 of file Reader.cc.

                                       {
    // Determine the format from the string (a file or file extension)
    const size_t lastdot = name.find_last_of(".");
    string fmt = Utils::toLower(lastdot == string::npos ? name : name.substr(lastdot+1));
    if (fmt == "gz") {
      #ifndef HAVE_LIBZ
      throw UserError("YODA was compiled without zlib support: can't read " + name);
      #endif
      const size_t lastbutonedot = (lastdot == string::npos) ? string::npos : name.find_last_of(".", lastdot-1);
      fmt = Utils::toLower(lastbutonedot == string::npos ? name : name.substr(lastbutonedot+1));
    }
    // Create the appropriate Reader
    #ifdef HAVE_HDF5
    if (Utils::startswith(fmt, "h5"))   return ReaderH5::create();
    #endif
    if (Utils::startswith(fmt, "yoda")) return ReaderYODA::create();
    if (Utils::startswith(fmt, "dat" )) return ReaderFLAT::create(); 
    if (Utils::startswith(fmt, "flat")) return ReaderFLAT::create();
    throw UserError("Format cannot be identified from string '" + name + "'");
  }

References YODA::ReaderFLAT::create(), YODA::ReaderH5::create(), and YODA::ReaderYODA::create().

Referenced by read(), and read().

mkTypeString() [1/2]

template<ssize_t DbnN, typename A , typename... As>

std::string YODA::mkTypeString

(

)

Helper function to construct the BinnedDbn and BinnedEstimate type names.

Definition at line 65 of file BinningUtils.h.

                           {
 
    constexpr size_t N = sizeof...(As)+1;
 
    if constexpr (all_CAxes<A, As...>::value) {
      if constexpr (DbnN < 0) {
        return "Estimate"+std::to_string(N)+"D";
      }
      if constexpr (DbnN == N+1) {
        return "Profile"+std::to_string(N)+"D";
      }
      if constexpr (DbnN == N) {
        return "Histo"+std::to_string(N)+"D";
      }
    }
 
    std::string type = "Binned";
    if (DbnN < 0)          type += "Estimate";
    else if (DbnN == N)    type += "Histo";
    else if (DbnN == N+1)  type += "Profile";
    else type += "Dbn" + std::to_string(DbnN);
 
    std::string axes = (TypeID<A>::name() + ... + (std::string{","} + TypeID<As>::name()));
 
    return (type + "<" + axes + ">");
  }

References YODA::TypeID< T >::name().

Referenced by mkTypeString().

mkTypeString() [2/2]

template<typename A , typename... As>

std::string YODA::mkTypeString

(

)

Same as above, but for non-Dbn bin contents.

Definition at line 94 of file BinningUtils.h.

{  return mkTypeString<-1, A, As...>(); }

References mkTypeString().

mkWriter()

Writer & YODA::mkWriter

(

const std::string &

format_name

)

Factory function to make a writer object by format name or a filename.

<

Todo:

Improve/remove... .ydat?

<

Todo:

Improve/remove... .ydat?

Definition at line 29 of file Writer.cc.

                                       {
    // Determine the format from the string (a file or file extension)
    const size_t lastdot = name.find_last_of(".");
    string fmt = Utils::toLower(lastdot == string::npos ? name : name.substr(lastdot+1));
    const bool compress = (fmt == "gz"s) || (fmt == "h5"s && enableH5compression);
    //cout << "***" << compress << endl;
    if (compress && fmt == "gz"s) {
      #ifndef HAVE_LIBZ
      throw UserError("YODA was compiled without zlib support: can't write " + name);
      #endif
      const size_t lastbutonedot = (lastdot == string::npos) ? string::npos : name.find_last_of(".", lastdot-1);
      fmt = Utils::toLower(lastbutonedot == string::npos ? name : name.substr(lastbutonedot+1));
    }
    // Create the appropriate Writer
    Writer* w = nullptr;
    #ifdef HAVE_HDF5
    if (Utils::startswith(fmt, "h5"))   w = &WriterH5::create();
    #endif
    if (Utils::startswith(fmt, "yoda")) w = &WriterYODA::create();
    else if (Utils::startswith(fmt, "dat" )) w = &WriterFLAT::create(); 
    else if (Utils::startswith(fmt, "flat")) w = &WriterFLAT::create();
    if (!w) throw UserError("Format cannot be identified from string '" + name + "'");
    w->useCompression(compress);
    return *w;
  }

References YODA::WriterFLAT::create(), YODA::WriterH5::create(), YODA::WriterYODA::create(), enableH5compression, and YODA::Writer::useCompression().

Referenced by write(), write(), write(), write(), write(), and write().

naiveChi2()

double YODA::naiveChi2 ( const std::vector< double > &  sample1, const std::vector< double > &  sample2, const std::vector< double > &  s1errors = std::vector<double>{}, const std::vector< double > &  s2errors = std::vector<double>{}  )

inline

Calculate the error-weighted chi2 statistic between two samples.

Note

This calculation is rather naive as it neglects the error breakdowns that may be available for the curves being compared. More sophisticated comparisons will require a separate analysis based on the Estimate objects utilising the full covariance information.

Definition at line 549 of file MathUtils.h.

                                                                          {},
                     const std::vector<double>& s2errors = std::vector<double>{}) {
    if (sample1.size() != sample2.size()) {
      throw RangeError("Inputs should have equal length!");
    }
    if (s1errors.size() && sample1.size() != s1errors.size()) {
      throw RangeError("Inputs should have equal length!");
    }
    if (s2errors.size() && sample2.size() != s2errors.size()) {
      throw RangeError("Inputs should have equal length!");
    }
    const size_t N = sample1.size();
    double chi2 = 0.0;
    for (size_t i = 0; i < N; ++i) {
      double temp = sqr(sample1[i] - sample2[i]);
      if (s1errors.size()) {
        temp /= sqr(s1errors[i]) + sqr(s2errors[i]);
      }
      chi2 += temp;
    }
    return chi2;
  }

naiveChi2reduced()

double YODA::naiveChi2reduced ( const std::vector< double > &  sample1, const std::vector< double > &  sample2, const std::vector< double > &  s1errors = std::vector<double>{}, const std::vector< double > &  s2errors = std::vector<double>{}  )

inline

Calculate the error-weighted reduced chi2 statistic between two samples.

Note

This calculation is rather naive as it neglects the error breakdowns that may be available for the curves being compared. More sophisticated comparisons will require a separate analysis based on the Estimate objects utilising the full covariance information.

Definition at line 579 of file MathUtils.h.

                                                                             {},
                        const std::vector<double>& s2errors = std::vector<double>{}) {
    if (sample1.empty()) throw RangeError("Inputs should not have 0 length!");
    return naiveChi2(sample1, sample2, s1errors, s2errors)/sample1.size();
  }

notNaN()

template<typename NUM >

std::enable_if_t< std::is_floating_point_v< NUM >, bool > YODA::notNaN ( NUM  val )

inline

Check if a number is non-NaN.

Definition at line 85 of file MathUtils.h.

{ return !std::isnan(val); }

nullifyIfDiscCoord() [1/2]

template<typename CoordT >

double YODA::nullifyIfDiscCoord	(	CoordT &&	,
		std::false_type	,
		double	null = 0.0
	)

Nullifies coordinate if it is discrete.

Definition at line 19 of file Binning.h.

                                                                          {
    return null;
  }

Referenced by containsNan().

nullifyIfDiscCoord() [2/2]

template<typename CoordT >

double YODA::nullifyIfDiscCoord	(	CoordT &&	coord,
		std::true_type	,
		double	= 0.0
	)

Definition at line 24 of file Binning.h.

                                                                          {
    return std::forward<CoordT>(coord);
  }

operator!=()

template<size_t N>

bool YODA::operator!= ( const PointBase< N > &  a, const PointBase< N > &  b  )

inline

Inequality test.

Definition at line 504 of file Point.h.

                                                                       {
    return !(a == b);
  }

operator*() [1/3]

Weights YODA::operator* ( const Weights &  first, const Weights &  second  )

inline

Multiply two weights.

Definition at line 268 of file Weights.h.

                                                                          {
    Weights tmp = first;
    tmp *= second;
    return tmp;
  }

operator*() [2/3]

Weights YODA::operator* ( const Weights &  w, double  a  )

inline

Multiply by a double.

Definition at line 290 of file Weights.h.

                                                         {
    return a * w;
  }

operator*() [3/3]

Weights YODA::operator* ( double  a, const Weights &  w  )

inline

Multiply by a double.

Definition at line 283 of file Weights.h.

                                                         {
    Weights tmp = w;
    tmp *= a;
    return tmp;
  }

operator+() [1/17]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator+ ( BinnedDbn< DbnN, AxisT... > &&  dbn, BinnedEstimate< AxisT... > &&  est  )

inline

Definition at line 1371 of file BinnedDbn.h.

                                                                               {
    return add(std::move(dbn), std::move(est));
  }

References add().

operator+() [2/17]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator+ ( BinnedDbn< DbnN, AxisT... > &&  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Definition at line 1359 of file BinnedDbn.h.

                                                                                    {
    return add(std::move(dbn), est);
  }

References add().

operator+() [3/17]

template<size_t DbnN, typename... AxisT>

BinnedDbn< DbnN, AxisT... > YODA::operator+ ( BinnedDbn< DbnN, AxisT... >  first, BinnedDbn< DbnN, AxisT... > &&  second  )

inline

Add two BinnedDbn objects.

Definition at line 1142 of file BinnedDbn.h.

                                                                                   {
    first += std::move(second);
    return first;
  }

operator+() [4/17]

template<size_t DbnN, typename... AxisT>

BinnedDbn< DbnN, AxisT... > YODA::operator+ ( BinnedDbn< DbnN, AxisT... >  first, const BinnedDbn< DbnN, AxisT... > &  second  )

inline

Definition at line 1149 of file BinnedDbn.h.

                                                                                        {
    first += second;
    return first;
  }

operator+() [5/17]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator+ ( BinnedEstimate< AxisT... >  first, BinnedEstimate< AxisT... > &&  second  )

inline

Add two BinnedEstimates.

Definition at line 1155 of file BinnedEstimate.h.

                                                                                 {
    first += std::move(second);
    return first;
  }

operator+() [6/17]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator+ ( BinnedEstimate< AxisT... >  first, const BinnedEstimate< AxisT... > &  second  )

inline

Add two BinnedEstimates.

Definition at line 1146 of file BinnedEstimate.h.

                                                                                      {
    first += second;
    return first;
  }

operator+() [7/17]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator+ ( const BinnedDbn< DbnN, AxisT... > &  dbn, BinnedEstimate< AxisT... > &&  est  )

inline

Definition at line 1365 of file BinnedDbn.h.

                                                                                    {
    return add(dbn, std::move(est));
  }

References add().

operator+() [8/17]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator+ ( const BinnedDbn< DbnN, AxisT... > &  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Definition at line 1353 of file BinnedDbn.h.

                                                                                         {
    return add(dbn, est);
  }

References add().

operator+() [9/17]

Weights YODA::operator+ ( const Weights &  first, const Weights &  second  )

inline

Add two weights.

Definition at line 254 of file Weights.h.

                                                                          {
    Weights tmp = first;
    tmp += second;
    return tmp;
  }

operator+() [10/17]

Counter YODA::operator+ ( Counter  first, const Counter &  second  )

inline

Add two counters.

Definition at line 369 of file Counter.h.

                                                                   {
    first += second;
    return first;
  }

operator+() [11/17]

Counter YODA::operator+ ( Counter  first, Counter &&  second  )

inline

Add two counters.

Definition at line 375 of file Counter.h.

                                                              {
    first += std::move(second);
    return first;
  }

operator+() [12/17]

template<size_t N>

DbnBase< N > YODA::operator+ ( DbnBase< N >  first, const DbnBase< N > &  second  )

inline

Add two DbnBases.

Definition at line 608 of file Dbn.h.

                                                                            {
    first += second;
    return first;
  }

operator+() [13/17]

template<size_t N>

DbnBase< N > YODA::operator+ ( DbnBase< N >  first, DbnBase< N > &&  second  )

inline

Add two DbnBases.

Definition at line 615 of file Dbn.h.

                                                                       {
    first += std::move(second);
    return first;
  }

operator+() [14/17]

Estimate YODA::operator+ ( Estimate  lhs, const Estimate &  rhs  )

inline

Add two Estimate objects.

Definition at line 660 of file Estimate.h.

                                                                 {
    lhs += rhs;
    return lhs;
  }

operator+() [15/17]

Estimate YODA::operator+ ( Estimate  lhs, Estimate &&  rhs  )

inline

Add two Estimate objects.

Definition at line 666 of file Estimate.h.

                                                            {
    lhs += std::move(rhs);
    return lhs;
  }

operator+() [16/17]

Estimate0D YODA::operator+ ( Estimate0D  lhs, const Estimate0D &  rhs  )

inline

Add two Estimate0D objects.

Definition at line 344 of file Estimate0D.h.

                                                                       {
    lhs += rhs;
    return lhs;
  }

operator+() [17/17]

Estimate0D YODA::operator+ ( Estimate0D  lhs, Estimate0D &&  rhs  )

inline

Add two Estimate0D objects.

Definition at line 350 of file Estimate0D.h.

                                                                  {
    lhs += std::move(rhs);
    return lhs;
  }

operator-() [1/17]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator- ( BinnedDbn< DbnN, AxisT... > &&  dbn, BinnedEstimate< AxisT... > &&  est  )

inline

Definition at line 1403 of file BinnedDbn.h.

                                                                               {
    return subtract(std::move(dbn), std::move(est));
  }

References subtract().

operator-() [2/17]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator- ( BinnedDbn< DbnN, AxisT... > &&  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Definition at line 1391 of file BinnedDbn.h.

                                                                                    {
    return subtract(std::move(dbn), est);
  }

References subtract().

operator-() [3/17]

template<size_t DbnN, typename... AxisT>

BinnedDbn< DbnN, AxisT... > YODA::operator- ( BinnedDbn< DbnN, AxisT... >  first, BinnedDbn< DbnN, AxisT... > &&  second  )

inline

Subtract one BinnedDbn object from another.

Definition at line 1158 of file BinnedDbn.h.

                                                                                   {
    first -= std::move(second);
    return first;
  }

operator-() [4/17]

template<size_t DbnN, typename... AxisT>

BinnedDbn< DbnN, AxisT... > YODA::operator- ( BinnedDbn< DbnN, AxisT... >  first, const BinnedDbn< DbnN, AxisT... > &  second  )

inline

Definition at line 1165 of file BinnedDbn.h.

                                                                                        {
    first -= second;
    return first;
  }

operator-() [5/17]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator- ( BinnedEstimate< AxisT... >  first, BinnedEstimate< AxisT... > &&  second  )

inline

Subtract two BinnedEstimates.

Definition at line 1172 of file BinnedEstimate.h.

                                                                                 {
    first -= std::move(second);
    return first;
  }

operator-() [6/17]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator- ( BinnedEstimate< AxisT... >  first, const BinnedEstimate< AxisT... > &  second  )

inline

Subtract two BinnedEstimates.

Definition at line 1164 of file BinnedEstimate.h.

                                                                                      {
    first -= second;
    return first;
  }

operator-() [7/17]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator- ( const BinnedDbn< DbnN, AxisT... > &  dbn, BinnedEstimate< AxisT... > &&  est  )

inline

Definition at line 1397 of file BinnedDbn.h.

                                                                                    {
    return subtract(dbn, std::move(est));
  }

References subtract().

operator-() [8/17]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator- ( const BinnedDbn< DbnN, AxisT... > &  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Definition at line 1385 of file BinnedDbn.h.

                                                                                         {
    return subtract(dbn, est);
  }

References subtract().

operator-() [9/17]

Weights YODA::operator- ( const Weights &  first, const Weights &  second  )

inline

Subtract two weights.

Definition at line 261 of file Weights.h.

                                                                          {
    Weights tmp = first;
    tmp -= second;
    return tmp;
  }

operator-() [10/17]

Counter YODA::operator- ( Counter  first, const Counter &  second  )

inline

Subtract two counters.

Definition at line 381 of file Counter.h.

                                                                   {
    first -= second;
    return first;
  }

operator-() [11/17]

Counter YODA::operator- ( Counter  first, Counter &&  second  )

inline

Subtract two counters.

Definition at line 387 of file Counter.h.

                                                              {
    first -= std::move(second);
    return first;
  }

operator-() [12/17]

template<size_t N>

DbnBase< N > YODA::operator- ( DbnBase< N >  first, const DbnBase< N > &  second  )

inline

Subtract one DbnBase from another one.

Definition at line 622 of file Dbn.h.

                                                                            {
    first -= second;
    return first;
  }

operator-() [13/17]

template<size_t N>

DbnBase< N > YODA::operator- ( DbnBase< N >  first, DbnBase< N > &&  second  )

inline

Subtract one DbnBase from another one.

Definition at line 629 of file Dbn.h.

                                                                       {
    first -= std::move(second);
    return first;
  }

operator-() [14/17]

Estimate YODA::operator- ( Estimate  lhs, const Estimate &  rhs  )

inline

Subtract two Estimate objects.

Definition at line 672 of file Estimate.h.

                                                                 {
    lhs -= rhs;
    return lhs;
  }

operator-() [15/17]

Estimate YODA::operator- ( Estimate  lhs, Estimate &&  rhs  )

inline

Subtract two Estimate objects.

Definition at line 678 of file Estimate.h.

                                                            {
    lhs -= std::move(rhs);
    return lhs;
  }

operator-() [16/17]

Estimate0D YODA::operator- ( Estimate0D  lhs, const Estimate0D &  rhs  )

inline

Subtract two Estimate0D objects.

Definition at line 356 of file Estimate0D.h.

                                                                       {
    lhs -= rhs;
    return lhs;
  }

operator-() [17/17]

Estimate0D YODA::operator- ( Estimate0D  lhs, Estimate0D &&  rhs  )

inline

Subtract two Estimate0D objects.

Definition at line 362 of file Estimate0D.h.

                                                                  {
    lhs -= std::move(rhs);
    return lhs;
  }

operator/() [1/27]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( BinnedDbn< DbnN, AxisT... > &&  dbn, BinnedEstimate< AxisT... > &&  est  )

inline

Definition at line 1435 of file BinnedDbn.h.

                                                                               {
    return divide(std::move(dbn), std::move(est));
  }

References divide().

operator/() [2/27]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( BinnedDbn< DbnN, AxisT... > &&  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Definition at line 1423 of file BinnedDbn.h.

                                                                                    {
    return divide(std::move(dbn), est);
  }

References divide().

operator/() [3/27]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( BinnedDbn< DbnN, AxisT... > &&  numer, BinnedDbn< DbnN, AxisT... > &&  denom  )

inline

Definition at line 1233 of file BinnedDbn.h.

                                                                                    {
    return divide(std::move(numer), std::move(denom));
  }

References divide().

operator/() [4/27]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( BinnedDbn< DbnN, AxisT... > &&  numer, const BinnedDbn< DbnN, AxisT... > &  denom  )

inline

Definition at line 1227 of file BinnedDbn.h.

                                                                                         {
    return divide(std::move(numer), denom);
  }

References divide().

operator/() [5/27]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( BinnedEstimate< AxisT... > &&  numer, BinnedEstimate< AxisT... > &&  denom  )

inline

Divide two BinnedEstimates.

Definition at line 1223 of file BinnedEstimate.h.

                                                                                  {
    return divide(std::move(numer), std::move(denom));
  }

References divide().

operator/() [6/27]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( BinnedEstimate< AxisT... > &&  numer, const BinnedEstimate< AxisT... > &  denom  )

inline

Divide two BinnedEstimates.

Definition at line 1209 of file BinnedEstimate.h.

                                                                                       {
    return divide(std::move(numer), denom);
  }

References divide().

operator/() [7/27]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( const BinnedDbn< DbnN, AxisT... > &  dbn, BinnedEstimate< AxisT... > &&  est  )

inline

Definition at line 1429 of file BinnedDbn.h.

                                                                                    {
    return divide(dbn, std::move(est));
  }

References divide().

operator/() [8/27]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( const BinnedDbn< DbnN, AxisT... > &  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Definition at line 1417 of file BinnedDbn.h.

                                                                                         {
    return divide(dbn, est);
  }

References divide().

operator/() [9/27]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( const BinnedDbn< DbnN, AxisT... > &  numer, BinnedDbn< DbnN, AxisT... > &&  denom  )

inline

Definition at line 1221 of file BinnedDbn.h.

                                                                                         {
    return divide(numer, std::move(denom));
  }

References divide().

operator/() [10/27]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( const BinnedDbn< DbnN, AxisT... > &  numer, const BinnedDbn< DbnN, AxisT... > &  denom  )

inline

Definition at line 1215 of file BinnedDbn.h.

                                                                                              {
    return divide(numer, denom);
  }

References divide().

operator/() [11/27]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( const BinnedEstimate< AxisT... > &  numer, BinnedEstimate< AxisT... > &&  denom  )

inline

Divide two BinnedEstimates.

Definition at line 1216 of file BinnedEstimate.h.

                                                                                       {
    return divide(numer, std::move(denom));
  }

References divide().

operator/() [12/27]

template<typename... AxisT>

BinnedEstimate< AxisT... > YODA::operator/ ( const BinnedEstimate< AxisT... > &  numer, const BinnedEstimate< AxisT... > &  denom  )

inline

Divide two BinnedEstimates.

Definition at line 1202 of file BinnedEstimate.h.

                                                                                            {
    return divide(numer, denom);
  }

References divide().

operator/() [13/27]

Estimate0D YODA::operator/ ( const Counter &  numer, const Counter &  denom  )

inline

Divide two Counter objects.

Definition at line 396 of file Counter.h.

                                                                            {
    return divide(numer, denom);
  }

References divide().

operator/() [14/27]

Estimate0D YODA::operator/ ( const Counter &  numer, Counter &&  denom  )

inline

Divide two Counter objects.

Definition at line 406 of file Counter.h.

                                                                       {
    return divide(numer, std::move(denom));
  }

References divide().

operator/() [15/27]

Estimate YODA::operator/ ( const Estimate &  numer, const Estimate &  denom  )

inline

Divide two Estimate objects.

Definition at line 745 of file Estimate.h.

                                                                            {
    return divide(numer, denom);
  }

References divide().

operator/() [16/27]

Estimate YODA::operator/ ( const Estimate &  numer, Estimate &&  denom  )

inline

Divide two Estimate objects.

Definition at line 755 of file Estimate.h.

                                                                       {
    return divide(numer, std::move(denom));
  }

References divide().

operator/() [17/27]

Estimate0D YODA::operator/ ( const Estimate0D &  numer, const Estimate0D &  denom  )

inline

Divide two Estimate0D objects.

Definition at line 378 of file Estimate0D.h.

                                                                                  {
    return divide(numer, denom);
  }

References divide().

operator/() [18/27]

Estimate0D YODA::operator/ ( const Estimate0D &  numer, Estimate0D &&  denom  )

inline

Divide two Estimate0D objects.

Definition at line 388 of file Estimate0D.h.

                                                                             {
    return divide(numer, std::move(denom));
  }

References divide().

operator/() [19/27]

Weights YODA::operator/ ( const Weights &  numer, const Weights &  denom  )

inline

Divide two weights.

Definition at line 275 of file Weights.h.

                                                                         {
    Weights tmp = numer;
    tmp /= denom;
    return tmp;
  }

operator/() [20/27]

Weights YODA::operator/ ( const Weights &  w, double  a  )

inline

Divide by a double.

Definition at line 295 of file Weights.h.

                                                         {
    Weights tmp = w;
    tmp /= a;
    return tmp;
  }

operator/() [21/27]

Estimate0D YODA::operator/ ( Counter &&  numer, const Counter &  denom  )

inline

Divide two Counter objects.

Definition at line 401 of file Counter.h.

                                                                       {
    return divide(std::move(numer), denom);
  }

References divide().

operator/() [22/27]

Estimate0D YODA::operator/ ( Counter &&  numer, Counter &&  denom  )

inline

Divide two Counter objects.

Definition at line 411 of file Counter.h.

                                                                  {
    return divide(std::move(numer), std::move(denom));
  }

References divide().

operator/() [23/27]

Weights YODA::operator/ ( double  a, const Weights &  w  )

inline

Divide a double by a Weights

Todo:

Is this really needed?

Definition at line 303 of file Weights.h.

                                                         {
    Weights tmp(w.keys(), a);
    tmp /= w;
    return tmp;
  }

References YODA::Weights::keys().

operator/() [24/27]

Estimate YODA::operator/ ( Estimate &&  numer, const Estimate &  denom  )

inline

Divide two Estimate objects.

Definition at line 750 of file Estimate.h.

                                                                       {
    return divide(std::move(numer), denom);
  }

References divide().

operator/() [25/27]

Estimate YODA::operator/ ( Estimate &&  numer, Estimate &&  denom  )

inline

Divide two Estimate objects.

Definition at line 760 of file Estimate.h.

                                                                  {
    return divide(std::move(numer), std::move(denom));
  }

References divide().

operator/() [26/27]

Estimate0D YODA::operator/ ( Estimate0D &&  numer, const Estimate0D &  denom  )

inline

Divide two Estimate0D objects.

Definition at line 383 of file Estimate0D.h.

                                                                             {
    return divide(std::move(numer), denom);
  }

References divide().

operator/() [27/27]

Estimate0D YODA::operator/ ( Estimate0D &&  numer, Estimate0D &&  denom  )

inline

Divide two Estimate0D objects.

Definition at line 393 of file Estimate0D.h.

                                                                        {
    return divide(std::move(numer), std::move(denom));
  }

References divide().

operator<()

template<size_t N>

bool YODA::operator< ( const PointBase< N > &  a, const PointBase< N > &  b  )

inline

Less-than operator used to sort points.

Definition at line 511 of file Point.h.

                                                                      {
    #define LT_IF_NOT_EQ(a,b) { if (!fuzzyEquals(a, b)) return a < b; }
    for (size_t i = 0; i < N; ++i) {
      LT_IF_NOT_EQ(a.vals()[i],        b.vals()[i]);
      LT_IF_NOT_EQ(a.errs()[i].first,  b.errs()[i].first);
      LT_IF_NOT_EQ(a.errs()[i].second, b.errs()[i].second);
    }
    #undef LT_IF_NOT_EQ
    return false;
  }

References YODA::PointBase< N >::errs(), LT_IF_NOT_EQ, and YODA::PointBase< N >::vals().

operator<<()

std::ostream & YODA::operator<< ( std::ostream &  out, const Weights &  w  )

inline

Standard text representaion.

Definition at line 313 of file Weights.h.

                                                                   {
    out << "{ ";
    for (Weights::const_iterator i = w.begin(); i != w.end(); ++i) {
      if (i != w.begin()) out << ", ";
      out << i->first << ": " << i->second;
    }
    out << "}";
    return out;
  }

References YODA::Weights::begin(), and YODA::Weights::end().

operator<=()

template<size_t N>

bool YODA::operator<= ( const PointBase< N > &  a, const PointBase< N > &  b  )

inline

Less-than-or-equals operator used to sort points.

Definition at line 524 of file Point.h.

                                                                       {
    if (a == b) return true;
    return a < b;
  }

operator==()

template<size_t N>

bool YODA::operator== ( const PointBase< N > &  a, const PointBase< N > &  b  )

inline

Equality test.

Definition at line 492 of file Point.h.

                                                                       {
    // Compare valitions
    for (size_t i = 0; i < N; ++i) {
      if ( !fuzzyEquals(a.vals()[i],        b.vals()[i]) )        return false;
      if ( !fuzzyEquals(a.errs()[i].first,  b.errs()[i].first))  return false;
      if ( !fuzzyEquals(a.errs()[i].second, b.errs()[i].second)) return false;
    }
    return true;
  }

References YODA::PointBase< N >::errs(), fuzzyEquals(), and YODA::PointBase< N >::vals().

operator>()

template<size_t N>

bool YODA::operator> ( const PointBase< N > &  a, const PointBase< N > &  b  )

inline

Greater-than operator used to sort points.

Definition at line 531 of file Point.h.

                                                                      {
    return !(a <= b);
  }

operator>=()

template<size_t N>

bool YODA::operator>= ( const PointBase< N > &  a, const PointBase< N > &  b  )

inline

Greater-than-or-equals operator used to sort points.

Definition at line 537 of file Point.h.

                                                                       {
    return !(a < b);
  }

pdfspace()

std::vector< double > YODA::pdfspace ( size_t  nbins, double  xmin, double  xmax, std::function< double(double)> &  fn, size_t  nsample = 10000  )

inline

Make a list of nbins + 1 values spaced with density ~ f(x) between xmin and end inclusive.

Todo:

fspace() for uniform sampling from f(x); requires ability to invert fn... how, in general?

The density function fn will be evaluated at nsample uniformly distributed points between xmin and xmax, its integral approximated via the Trapezium Rule and used to normalize the distribution, and nbins + 1 edges then selected to (approximately) divide into bins each containing fraction 1/nbins of the integral.

Note

The function fn does not need to be a normalized pdf, but it should be non-negative. Any negative values returned by fn(x) will be truncated to zero and contribute nothing to the estimated integral and binning density.

The arg ordering and the meaning of the nbins variable is "histogram-like", as opposed to the Numpy/Matlab version, and the xmin and xmax arguments are expressed in "normal" space, rather than in the function-mapped space as with Numpy/Matlab.

The naming of this function differs from the other, Matlab-inspired ones: the bin spacing is uniform in the CDF of the density function given, rather than in the function itself. For most use-cases this is more intuitive.

Definition at line 328 of file MathUtils.h.

                                                                                                                                   {
    const double dx = (xmax-xmin)/(double)nsample;
    const std::vector<double> xs = linspace(nsample, xmin, xmax);
    std::vector<double> ys(0, nsample);
    auto posfn = [&](double x){return std::max(fn(x), 0.0);};
    std::transform(xs.begin(), xs.end(), ys.begin(), posfn);
    std::vector<double> areas; areas.reserve(nsample);
    double areasum = 0;
    for (size_t i = 0; i < ys.size()-1; ++i) {
      const double area = (ys[i] + ys[i+1])*dx/2.0;
      areas[i] = area;
      areasum += area;
    }
    const double df = areasum/(double)nbins;
    std::vector<double> xedges{xmin}; xedges.reserve(nbins+1);
    double fsum = 0;
    for (size_t i = 0; i < nsample-1; ++i) {
      fsum += areas[i];
      if (fsum > df) {
        fsum = 0;
        xedges.push_back(xs[i+1]);
      }
    }
    xedges.push_back(xmax);
    assert(xedges.size() == nbins+1);
    return xedges;
  }

References linspace().

read() [1/4]

std::vector< AnalysisObject * > YODA::read ( const std::string &  filename, const std::string &  match = "", const std::string &  unmatch = ""  )

inline

Read in a collection of objects from file filename.

This version returns a vector by value, involving copying, and is hence less CPU efficient than the alternative version where a vector is filled by reference. The appropriate format reader will be determined from the filename.

Definition at line 98 of file IO.h.

                                                                          {
    std::vector<AnalysisObject*> rtn;
    read(filename, rtn, match, unmatch);
    return rtn;
  }

References read().

read() [2/4]

void YODA::read ( const std::string &  filename, std::vector< AnalysisObject * > &  aos, const std::string &  match = "", const std::string &  unmatch = ""  )

inline

Read in a collection of objects objs from file filename.

This version fills (actually, appends to) a supplied vector, avoiding copying, and is hence CPU efficient. The appropriate format reader will be determined from the filename.

Todo:

Use SFINAE magic to allow ~arbitrary collection<AnalysisObject*> (with push_back()?) to be passed

Definition at line 85 of file IO.h.

                                                                               {
    Reader& r = mkReader(filename);
    r.read(filename, aos, match, unmatch);
  }

References mkReader(), and YODA::Reader::read().

Referenced by read(), and read().

read() [3/4]

std::vector< AnalysisObject * > YODA::read ( std::istream &  is, const std::string &  fmt, const std::string &  match = "", const std::string &  unmatch = ""  )

inline

Read in a collection of objects from stream is, expecting format fmt.

This version returns a vector by value, involving copying, and is hence less CPU efficient than the alternative version where a vector is filled by reference.

Definition at line 129 of file IO.h.

                                                                                            {
    std::vector<AnalysisObject*> rtn;
    read(is, rtn, fmt, match, unmatch);
    return rtn;
  }

References read().

read() [4/4]

void YODA::read ( std::istream &  is, std::vector< AnalysisObject * > &  aos, const std::string &  fmt, const std::string &  match = "", const std::string &  unmatch = ""  )

inline

Read in a collection of objects objs from stream is, expecting format fmt.

This version fills (actually, appends to) a supplied vector, avoiding copying, and is hence CPU efficient.

Todo:

Use SFINAE magic to allow ~arbitrary collection<AnalysisObject*> (with push_back()?) to be passed

Definition at line 118 of file IO.h.

                                                                                                 {
    Reader& r = mkReader(fmt);
    r.read(is, aos, match, unmatch);
  }

References mkReader(), and YODA::Reader::read().

RMS() [1/2]

double YODA::RMS ( const double  sumWX2, const double  sumW, const double  sumW2  )

inline

Calculate the weighted RMS of a sample.

Definition at line 495 of file MathUtils.h.

                                                                                {
    // Weighted RMS defined as
    // rms = sqrt(sum{w x^2} / sum{w})
    const double effN = effNumEntries(sumW, sumW2);
    if (effN == 0)  return std::numeric_limits<double>::quiet_NaN();
    const double meanSq = sumWX2 / sumW;
    return std::sqrt(meanSq);
  }

References effNumEntries().

Referenced by YODA::DbnBase< N >::RMS(), RMS(), YODA::XDbnMixin< Derived >::xRMS(), YODA::YDbnMixin< Derived >::yRMS(), and YODA::ZDbnMixin< Derived >::zRMS().

RMS() [2/2]

double YODA::RMS ( const std::vector< double > &  sample, const std::vector< double > &  weights  )

inline

Calculate the weighted RMS of a sample.

Definition at line 505 of file MathUtils.h.

                                                      {
    if (sample.size() != weights.size())  throw RangeError("Inputs should have equal length!");
    double sumWX2 = 0., sumW = 0., sumW2 = 0.;
    for (size_t i = 0; i < sample.size(); ++i) {
      sumW   += weights[i];
      sumW2  += sqr(weights[i]);
      sumWX2 += weights[i]*sqr(sample[i]);
    }
    return RMS(sumWX2, sumW, sumW2);
  }

References RMS(), and sqr().

sign() [1/3]

int YODA::sign ( double  val )

inline

Find the sign of a number.

Definition at line 228 of file MathUtils.h.

                              {
    if (isZero(val)) return ZERO;
    const int valsign = (val > 0) ? PLUS : MINUS;
    return valsign;
  }

References isZero(), MINUS, PLUS, and ZERO.

sign() [2/3]

int YODA::sign ( int  val )

inline

Find the sign of a number.

Definition at line 235 of file MathUtils.h.

                           {
    if (val == 0) return ZERO;
    return (val > 0) ? PLUS : MINUS;
  }

References MINUS, PLUS, and ZERO.

sign() [3/3]

int YODA::sign ( long  val )

inline

Find the sign of a number.

Definition at line 241 of file MathUtils.h.

                            {
    if (val == 0) return ZERO;
    return (val > 0) ? PLUS : MINUS;
  }

References MINUS, PLUS, and ZERO.

sqr()

template<typename NUM >

NUM YODA::sqr ( NUM  a )

inline

Named number-type squaring operation.

Definition at line 216 of file MathUtils.h.

                        {
    return a*a;
  }

Referenced by add_quad(), YODA::EstimateStorage< AxisT >::covarianceMatrix(), divide(), efficiency(), efficiency(), efficiency(), effNumEntries(), effNumEntries(), YODA::DbnBase< N >::fill(), YODA::FillableStorage< FillDim, BinContentT, AxisT >::fill(), mkIntegralEff(), RMS(), YODA::DbnBase< N >::scale(), YODA::DbnBase< N >::scaleW(), variance(), and variance().

stdDev() [1/2]

double YODA::stdDev ( const double  sumWX, const double  sumW, const double  sumWX2, const double  sumW2  )

inline

Calculate the weighted standard deviation of a sample.

Definition at line 464 of file MathUtils.h.

                                                                {
    return std::sqrt(variance(sumWX, sumW, sumWX2, sumW2));
  }

References variance().

Referenced by YODA::XDbnMixin< Derived >::xStdDev(), YODA::XStatsMixin< Derived >::xStdDev(), YODA::YDbnMixin< Derived >::yStdDev(), YODA::YStatsMixin< Derived >::yStdDev(), YODA::ZDbnMixin< Derived >::zStdDev(), and YODA::ZStatsMixin< Derived >::zStdDev().

stdDev() [2/2]

double YODA::stdDev ( const std::vector< double > &  sample, const std::vector< double > &  weights  )

inline

Calculate the weighted variance of a sample.

Definition at line 470 of file MathUtils.h.

                                                         {
    return std::sqrt(variance(sample, weights));
  }

References variance().

stdErr() [1/2]

double YODA::stdErr ( const double  sumWX, const double  sumW, const double  sumWX2, const double  sumW2  )

inline

Calculate the weighted standard error of a sample.

Definition at line 476 of file MathUtils.h.

                                                                {
    const double effN = effNumEntries(sumW, sumW2);
    if (effN == 0)  return std::numeric_limits<double>::quiet_NaN();
    const double var = variance(sumWX, sumW, sumWX2, sumW2);
    return std::sqrt(var / effN);
  }

References effNumEntries(), and variance().

Referenced by YODA::DbnBase< N >::relStdErr(), YODA::DbnBase< N >::stdErr(), YODA::XDbnMixin< Derived >::xStdErr(), YODA::XStatsMixin< Derived >::xStdErr(), YODA::YDbnMixin< Derived >::yStdErr(), YODA::YStatsMixin< Derived >::yStdErr(), zipProfiles(), YODA::ZDbnMixin< Derived >::zStdErr(), and YODA::ZStatsMixin< Derived >::zStdErr().

stdErr() [2/2]

double YODA::stdErr ( const std::vector< double > &  sample, const std::vector< double > &  weights  )

inline

Calculate the weighted variance of a sample.

Definition at line 485 of file MathUtils.h.

                                                          {
    if (sample.size() != weights.size())  throw RangeError("Inputs should have equal length!");
    const double effN = effNumEntries(weights);
    if (effN == 0)  return std::numeric_limits<double>::quiet_NaN();
    const double var = variance(sample, weights);
    return std::sqrt(var / effN);
  }

References effNumEntries(), and variance().

subtract() [1/2]

template<size_t DbnN, typename... AxisT>

BinnedEstimate< AxisT... > YODA::subtract ( const BinnedDbn< DbnN, AxisT... > &  dbn, const BinnedEstimate< AxisT... > &  est  )

inline

Calculate the subtraction of a BinnedEstimate from a BinnedDbn.

Definition at line 1379 of file BinnedDbn.h.

                                                                                      {
    return dbn.mkEstimate() - est;
  }

References YODA::DbnStorage< DbnN, AxisT >::mkEstimate().

Referenced by add(), asymm(), operator-(), operator-(), operator-(), operator-(), and variance().

subtract() [2/2]

double YODA::subtract ( double  a, double  b, double  tolerance = 1e-5  )

inline

Subtract two numbers with FP fuzziness.

Definition at line 247 of file MathUtils.h.

                                                                      {
    if (fuzzyEquals(a,b,tolerance))  return 0.;
    return a - b;
  }

References fuzzyEquals().

transform() [1/6]

template<typename... AxisT, typename FN >

void YODA::transform ( BinnedEstimate< AxisT... > &  est, const FN &  fn  )

inline

Definition at line 1281 of file BinnedEstimate.h.

                                                                     {
    transform(est, Trf<1>(fn));
  }

References transform().

transform() [2/6]

template<typename... AxisT>

void YODA::transform ( BinnedEstimate< AxisT... > &  est, const Trf< 1 > &  fn  )

inline

Definition at line 1274 of file BinnedEstimate.h.

                                                                         {
    for (auto& b : est.bins(true, true)) {
      b.transform(fn);
    }
  }

References YODA::BinnedStorage< BinContentT, AxisT >::bins().

Referenced by transform(), transform(), transform(), transformX(), transformY(), and transformZ().

transform() [3/6]

template<typename FN >

void YODA::transform ( Estimate0D &  est, const FN &  fn  )

inline

Definition at line 333 of file Estimate0D.h.

                                                       {
    transform(est, Trf<1>(fn));
  }

References transform().

transform() [4/6]

void YODA::transform ( Estimate0D &  est, const Trf< 1 > &  fn  )

inline

Definition at line 328 of file Estimate0D.h.

                                                           {
    est.transform(fn);
  }

References YODA::Estimate::transform().

transform() [5/6]

template<size_t N, typename FN >

void YODA::transform ( ScatterND< N > &  s, const FN &  fn, const size_t  i  )

inline

Definition at line 877 of file Scatter.h.

                                                                       {
    transform(s, Trf<N>(fn), i);
  }

References transform().

transform() [6/6]

template<size_t N>

void YODA::transform ( ScatterND< N > &  s, const Trf< N > &  fn, const size_t  i  )

inline

Definition at line 870 of file Scatter.h.

                                                                           {
    for (auto& p : s.points()) {
      p.transform(i, fn);
    }
  }

References YODA::ScatterND< N >::points().

transformX()

template<size_t N, typename FN >

void YODA::transformX ( ScatterND< N > &  s, const FN &  fn  )

inline

Definition at line 882 of file Scatter.h.

                                                        {
    transform(s, fn, 0);
  }

References transform().

transformY()

template<size_t N, typename FN >

void YODA::transformY ( ScatterND< N > &  s, const FN &  fn  )

inline

Definition at line 887 of file Scatter.h.

                                                        {
    transform(s, fn, 1);
  }

References transform().

transformZ()

template<size_t N, typename FN >

void YODA::transformZ ( ScatterND< N > &  s, const FN &  fn  )

inline

Definition at line 892 of file Scatter.h.

                                                        {
    transform(s, fn, 2);
  }

References transform().

variance() [1/2]

double YODA::variance ( const double  sumWX, const double  sumW, const double  sumWX2, const double  sumW2  )

inline

Calculate the weighted variance of a sample.

Weighted variance defined as sig2 = ( sum(wx**2) * sum(w) - sum(wx)**2 ) / ( sum(w)**2 - sum(w**2) ) see http://en.wikipedia.org/wiki/Weighted_mean

Todo:

Isn't this sensitive to the overall scale of the weights? Shouldn't it check if den is bigger then num by a set number of orders of magnitude and vice versa?

We take the modulus of the weighted variance since the ratio can be negative with weighted means

Todo:

Is this the correct approach? There is no information online other than "weights are non-negative"...

Definition at line 427 of file MathUtils.h.

                                                                  {
    const double num = subtract(sumWX2*sumW, sqr(sumWX));
    const double den = subtract(sqr(sumW), sumW2);
    // if (fabs(num) < 1e-10 && fabs(den) < 1e-10) {
    //   return std::numeric_limits<double>::quiet_NaN();
    // }
    return den? fabs(num/den): std::numeric_limits<double>::quiet_NaN();
  }

References sqr(), and subtract().

Referenced by stdDev(), stdDev(), stdErr(), stdErr(), YODA::DbnBase< N >::variance(), variance(), YODA::XDbnMixin< Derived >::xVariance(), YODA::XStatsMixin< Derived >::xVariance(), YODA::YDbnMixin< Derived >::yVariance(), YODA::YStatsMixin< Derived >::yVariance(), YODA::ZDbnMixin< Derived >::zVariance(), and YODA::ZStatsMixin< Derived >::zVariance().

variance() [2/2]

double YODA::variance ( const std::vector< double > &  sample, const std::vector< double > &  weights  )

inline

Calculate the weighted variance of a sample.

Definition at line 445 of file MathUtils.h.

                                                           {
    if (sample.size() != weights.size())  throw RangeError("Inputs should have equal length!");
    if (fuzzyLessEquals(effNumEntries(weights), 1.0)) {
       //throw LowStatsError("Requested variance of a distribution with only one effective entry");
       return std::numeric_limits<double>::quiet_NaN();
    }
    double sumWX = 0., sumW = 0.;
    double sumWX2 = 0., sumW2 = 0.;
    for (size_t i = 0; i < sample.size(); ++i) {
      sumW   += weights[i];
      sumWX  += weights[i]*sample[i];
      sumW2  += sqr(weights[i]);
      sumWX2 += weights[i]*sqr(sample[i]);
    }
    return variance(sumWX, sumW, sumWX2, sumW2);
  }

References effNumEntries(), fuzzyLessEquals(), sqr(), and variance().

version()

std::string YODA::version ( )

inline

Namespaced version string function.

Definition at line 25 of file YodaConfig.h.

                             {
    return YODA_VERSION;
  }

References YODA_VERSION.

write() [1/6]

void YODA::write ( const std::string &  filename, const AnalysisObject &  ao, int  precision = -1  )

inline

Write out object ao to file filename.

Definition at line 19 of file IO.h.

                                                                                           {
    Writer& w = mkWriter(filename);
    if (precision > 0) w.setPrecision(precision);
    w.write(filename, ao);
  }

References mkWriter(), YODA::Writer::setPrecision(), and YODA::Writer::write().

Referenced by YODA::H5DataSetWriter< T >::writeSlice().

write() [2/6]

template<typename AOITER >

void YODA::write ( const std::string &  filename, const AOITER &  begin, const AOITER &  end, int  precision = -1  )

inline

Write out the objects specified by start iterator begin and end iterator end to file filename.

Definition at line 36 of file IO.h.

                                                                                                         {
    Writer& w = mkWriter(filename);
    if (precision > 0) w.setPrecision(precision);
    w.write(filename, begin, end);
  }

References mkWriter(), YODA::Writer::setPrecision(), and YODA::Writer::write().

write() [3/6]

template<typename RANGE >

void YODA::write ( const std::string &  filename, const RANGE &  aos, int  precision = -1  )

inline

Write out a collection of objects objs to file filename.

Definition at line 27 of file IO.h.

                                                                                   {
    Writer& w = mkWriter(filename);
    if (precision > 0) w.setPrecision(precision);
    w.write(filename, aos);
  }

References mkWriter(), YODA::Writer::setPrecision(), and YODA::Writer::write().

write() [4/6]

void YODA::write ( std::ostream &  os, const AnalysisObject &  ao, const std::string &  fmt, int  precision = -1  )

inline

Write out object ao to stream os with format fmt.

Definition at line 49 of file IO.h.

                                                                                                      {
    Writer& w = mkWriter(fmt);
    if (precision > 0) w.setPrecision(precision);
    w.write(os, ao);
  }

References mkWriter(), YODA::Writer::setPrecision(), and YODA::Writer::write().

write() [5/6]

template<typename AOITER >

void YODA::write ( std::ostream &  os, const AOITER &  begin, const AOITER &  end, const std::string &  fmt, int  precision = -1  )

inline

Write out the objects specified by start iterator begin and end iterator end to file filename.

Definition at line 66 of file IO.h.

                                                                                                                    {
    Writer& w = mkWriter(fmt);
    if (precision > 0) w.setPrecision(precision);
    w.write(os, begin, end);
  }

References mkWriter(), YODA::Writer::setPrecision(), and YODA::Writer::write().

write() [6/6]

template<typename RANGE >

void YODA::write ( std::ostream &  os, const RANGE &  aos, const std::string &  fmt, int  precision = -1  )

inline

Write out a collection of objects objs to file filename.

Definition at line 57 of file IO.h.

                                                                                              {
    Writer& w = mkWriter(fmt);
    if (precision > 0) w.setPrecision(precision);
    w.write(os, aos);
  }

References mkWriter(), YODA::Writer::setPrecision(), and YODA::Writer::write().

zipProfiles()

template<size_t DbnN, typename... AxisT, typename... Args, typename = std::enable_if_t<(DbnN == sizeof...(AxisT)+1 && (std::is_same_v<BinnedDbn<DbnN, AxisT...>, Args> && ...))>>

ScatterND< sizeof...(Args)+1 > YODA::zipProfiles	(	const BinnedDbn< DbnN, AxisT... > &	p1,
		Args &&...	others,
		const std::string &	path = ""
	)

Zip profile objects of the same type into a combined scatter object.

The resulting object has as many points as profile bins and whose central values are given by the means along the unbinned profile axes with means of first profile corresponding to x-coordinate, means of second profile corresponding to y-coordinate etc.

Note

The BinnedDbn objects must be profiles and have the same axis config.

Definition at line 1451 of file BinnedDbn.h.

                                                                       {
 
    // Check profiles have the same binning
    if ( !((p1 == others) && ...) )
      throw BinningError("Requested zipping of profiles with incompatible binning!");
 
    // Construct resulting Scatter whose coordinates
    // are given by the unbinned means
    constexpr size_t N = sizeof...(Args)+1;
    ScatterND<N> rtn;
    rtn.setAnnotation("Path", path);
    for (const auto& b1 : p1.bins()) {
      typename ScatterND<N>::NdVal vals = { b1.mean(DbnN), others.bin(b1.binIndex()).mean(DbnN) ... };
      typename ScatterND<N>::NdVal errs = { b1.stdErr(DbnN), others.bin(b1.binIndex()).stdErr(DbnN) ... };
      rtn.addPoint(vals, errs);
    }
    return rtn;
  }

References YODA::ScatterND< N >::addPoint(), YODA::BinnedStorage< BinContentT, AxisT >::bins(), mean(), YODA::AnalysisObject::setAnnotation(), and stdErr().

Variable Documentation

BISECT_LINEAR_THRESHOLDlc

const size_t YODA::BISECT_LINEAR_THRESHOLDlc = 32

Definition at line 29 of file BinnedAxis.h.

enableH5compression

bool YODA::enableH5compression = Utils::getEnvParam("YODA_HDF5_COMPRESSION", true)

static

Definition at line 28 of file Writer.h.

Referenced by mkWriter(), and YODA::Writer::write().

fuzzyEqComp

std::function<bool(const double, const double)> YODA::fuzzyEqComp

static

Initial value:

=
    [](const double& lhs, const double& rhs) { return fuzzyEquals(lhs, rhs); }

Comparator wrapper to use with STL algorithms, e.g. std::equal etc.

Definition at line 115 of file MathUtils.h.

                                             { return fuzzyEquals(lhs, rhs); };

HALFPI

const double YODA::HALFPI = M_PI_2

static

A pre-defined value of .

Definition at line 48 of file MathUtils.h.

isCIterable

template<typename... T>

constexpr bool YODA::isCIterable = std::conjunction<CIterable<T>...>::value

inlineconstexpr

Definition at line 54 of file Traits.h.

isIterable

template<typename... T>

constexpr bool YODA::isIterable = std::conjunction<Iterable<T>...>::value

inlineconstexpr

Definition at line 44 of file Traits.h.

MAXDOUBLE

const double YODA::MAXDOUBLE = DBL_MAX

static

Pre-defined numeric type limits

Deprecated:

Prefer the standard DBL/INT_MAX

Definition at line 38 of file MathUtils.h.

MAXINT

const double YODA::MAXINT = INT_MAX

static

Definition at line 39 of file MathUtils.h.

PI

const double YODA::PI = M_PI

static

A pre-defined value of .

Definition at line 42 of file MathUtils.h.

SEARCH_SIZElc

const size_t YODA::SEARCH_SIZElc = 16

Definition at line 28 of file BinnedAxis.h.

Referenced by YODA::Axis< T, isCAxis< T > >::index().

TWOPI

const double YODA::TWOPI = 2*M_PI

static

A pre-defined value of .

Definition at line 45 of file MathUtils.h.

YODA_FORMAT_VERSION

const int YODA::YODA_FORMAT_VERSION = 3

static

YODA text-format version

• V1/empty = make-plots annotations style
• V2 = YAML annotations
• V3 = YODA2 types

Definition at line 28 of file WriterYODA.cc.

YODA_H5_FORMAT_VERSION

const size_t YODA::YODA_H5_FORMAT_VERSION = 1

static

YODA text-format version

• V1 = H5 format for YODA2 types

Definition at line 27 of file WriterH5.cc.

Referenced by YODA::WriterH5::writeAOS().